Module: Bit Operations (C++)


Problem

6/13

Determining the sign of a number

Theory Click to read/hide

Bit operations

All numbers in the computer memory are stored in binary form, i.e. in the form of a sequence of 0 and 1. To store numbers in computer memory, a finite number of bits are used. Because of this number, the computer has a limited range, and the calculation results may be inaccurate. An integer can be stored in 8, 16, 32, or 64 bits of memory. Each additional bit expands the range of possible values ​​by 2. 
Operations with positive and negative numbers are performed in the processor using the same algorithms.

With the help of bitwise logical operations, you can control individual bits of the registers of the processor and external devices. 
 
C++ operation Destination
a & b Bitwise And for a and b
a | b Bitwise OR for a and b
a ^ b X OR for a and b
~a Bit inversion for a
a << b Bitwise shift left of a to b
a >> b Bitwise right shift of a to b



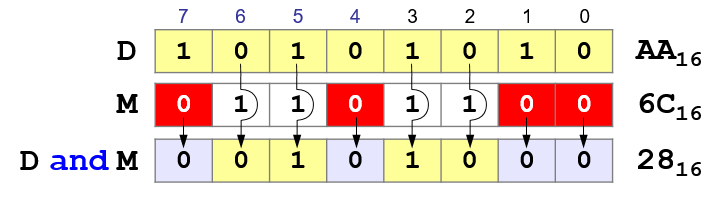
Operation AND
Using the operation "AND" you can reset (set to zero) bits for which the mask is 0! 
 
Mask – a constant that defines the scope of the logical operation on the bits of a multi-bit number.

D - data, M - mask

 

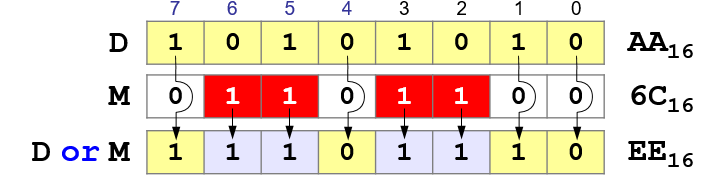
Operation OR
The operation "OR" can be used to write a 1 to the bits for which the mask is 1!

 

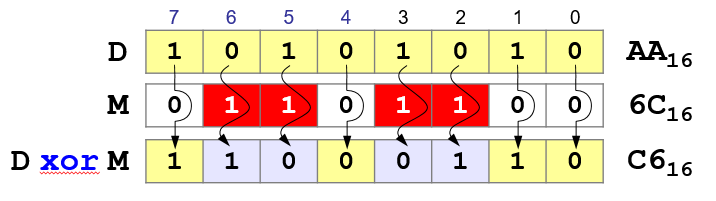
Operation exclusive OR
Using the operation "XOR" you can invert bits for which the mask is 1!


 

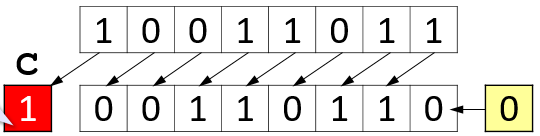
Shift Left
A logical (bitwise) left shift by 1 bit doubles a positive integer.

 

Shift Right
Boolean (bitwise) .shift right by 1  divides a positive integer by 2.


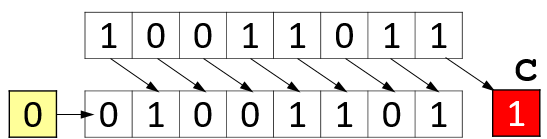
Since a right shift sets the sign bit on the vacated positions, the sign of the number x can be determined by right-shifting the entire length of the variable.

Problem

Let the number x be given. Determine the sign of the number.

Add the missing piece of code to the program.
 
Examples
# Input Output
1 10 1
2 -10 -1
3 0 0

time 1000 ms
memory 256 Mb
Rules for program design and list of errors in automatic problem checking

Teacher commentary

Insert the missing code snippets
C++
Write the program below 
#include <iostream>
using namespace std;

int getSign(int x) {
	int mask;  
if (x != 0)
		mask = 1;
	else
		mask = 0;  
}

int main()
{
	int x;
	cin >> x;
	cout << getSign(x);
	return 0;
}

     

Program check result

To check the solution of the problem, you need to register or log in!