To understand recursion, you need to understand recursion...
Iteration in programming — in a broad sense — organization of data processing, in which actions are repeated many times, without leading to calls to themselves (unlike %BA%D1%83%D1%80%D1%81%D0%B8%D1%8F" title="Recursion">Recursions). In the narrow sense — one step cyclic data processing process.
Often iterative algorithms at the current step (iteration) use the result of the same operation or action calculated at previous steps. One example of such calculations is the calculation of recurrence relations.
A simple example of a recursive value is the factorial:
\(N!=1 \cdot 2 \cdot 3 \cdot \ ... \ \cdot N\)
The calculation of the value at each step (iteration) is
\(N=N \cdot i\) . When calculating the value of
\(N\), we take the already stored value
\(N\).< br />
The factorial of a number can also be described using the
recurrent formula:
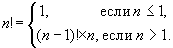
You may notice that this description is nothing more than a recursive function.
Here the first line (
\(n <= 1\)) — this is the base case (end condition of the recursion) and the second line is the transition to the next step.
| The recursive factorial function would look like this |
Compare the algorithm for finding the factorial in the usual, non-recursive way |
function Factorial(n: integer): integer;
begin
if n > 1 then
Factorial := n * Factorial(n - 1)
else
Factorial := 1;
end; |
x := 1;
for i := 2 to n do
x := x * i;
writeln(x); |
It should be understood that function calls involve some additional overhead, so a non-recursive factorial calculation will be slightly faster.
Conclusion: where you can write a program with a simple iterative algorithm, without recursion, then you need to write without recursion. But still, there is a large class of problems where the computational process is implemented only by recursion.
On the other hand, recursive algorithms are often more understandable.