Module: Spanning Trees: Kruskal's Algorithm


Problem

1/4

Алгоритм Крускала: Начало

Theory Click to read/hide

Пример минимального остовного дерева в графе с указанными весами ребер: 


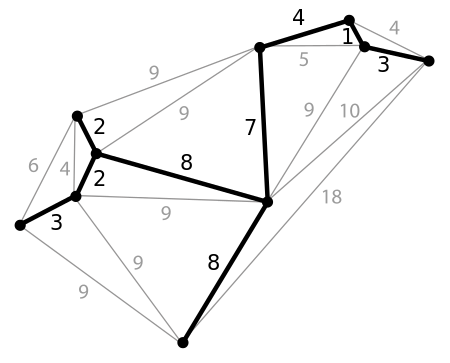
Алгоритм Крускала:

1) Сортиртируем ребра по весу  в порядке неубывания.
2) Формируем список из n деревьев ( каждая вершина это дерево ).
3)  Запускаем процесс объединения этих деревьев в минимальное остовное дерево:
      перебираются все рёбра и если у текущего ребра его концы принадлежат разным поддеревьям, то эти поддеревья объединяются.
4) По окончании перебора всех рёбер все вершины окажутся принадлежащими одному поддереву.

Problem

Требуется найти в связном графе остовное дерево минимального веса.
 
Формат входных данных:
 
Первая строка входного файла содержит два натуральных числа N, M - количество вершин и ребер графа соответственно. Следующие m строк содержат описание ребер по одному на строке. Ребро номер i описывается тремя натуральными числами Bi, Ei, Wi номера концов ребра и его вес соответственно (1 <= Bi, Ei <= N, 0 <= Wi <= 232-1. N <= 10, M <= 10).
 
Формат выходных данных:
 
Единственная строка выходного файла должна содержать одно натуральное число - вес минимального остовного дерева. 
 
Ввод Вывод
4 4
1 2 1
2 3 2
3 4 5
4 1 4
 7

time 1000 ms
memory 32 Mb
Rules for program design and list of errors in automatic problem checking

Teacher commentary

Insert the missing code snippets
C++
Write the program below 
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;

struct edge
{
	int l,a,b;
};

bool cmp(const edge &a, const edge &b)
{
    return a.l < b.l;
}

int main()
{
	int m, n;
	cin >> n >> m;

	vector < edge > g(m);

	for (int i = 0; i < m; i++)
	{
		int a, b, l;
		cin >> a >> b >>l;
		edge e;
                e.l = l; e.a= a-1; e.b = b-1;
		g[i] = e;
	}
	long long cost = 0;
	vector < pair<int, int> > res;

	sort(g.begin(), g.end(),cmp);
	vector<int> tree_id(n);
	for (int i = 0; i < n; ++i)
		tree_id[i] = i;
	for (int i = 0; i < m; ++i)
	{
		int a = g[i].a, b = g[i].b, l = g[i].l;
		if (tree_id[a] != tree_id[b])
		{        
			res.push_back(make_pair(a, b));
			int old_id = tree_id[b], new_id = tree_id[a];
			for (int j = 0; j < n; ++j)
				if (tree_id[j] == old_id)
					tree_id[j] = new_id;
		}
	}

	cout << cost;
	return 0;
}

     

Program check result

To check the solution of the problem, you need to register or log in!