Insert sort
Insertion sort (Insertion sort) — ;sorting algorithm in which the elements of the input sequence are looked up one at a time, and each new incoming element is placed in the appropriate place among the previously sorted elements.
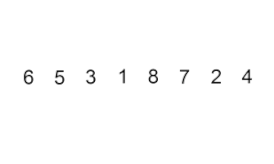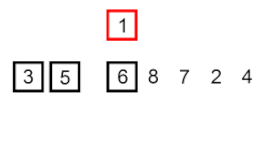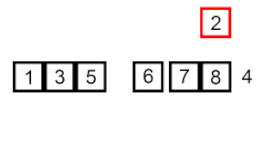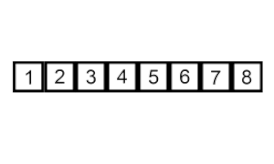
Insert sort – it is a very simple but inefficient algorithm that nevertheless has several specific advantages that make it relevant even after many other generally more efficient algorithms have been developed.
With insertion sort, you don't have to have the entire array up front before sorting. The algorithm can receive one element at a time during sorting. This is very handy if we need to add more elements during sorting. The algorithm will insert the new element at the right place without "re-executing" sorting the entire array.
Insertion sort can be used in practice due to its efficiency on small (~10 elements) datasets.
The problem is this: there is a part of the array that is already sorted, and you want to insert the remaining elements of the array into the sorted part, while maintaining order. To do this, at each step of the algorithm, we select one of the input data elements and insert it at the desired position in the already sorted part of the array, until the entire input data set is sorted. The method of selecting the next element from the input array is arbitrary, but usually (and in order to obtain a stable sorting algorithm), elements are inserted in the order of their appearance in the input array.
Algorithmic implementation of this algorithm
// The null element is considered to be an already sorted sequence.
// Therefore, the loop starts from 1
LOOP FOR I=1 TO N-1 STEP 1
X=A[I]
J=I
WHEN J>0 AND A[J-1]>X //looking for a place to insert
EXCHANGE A[J],A[J-1]
J=J-1
END BYE
A[J]=X
NEXT I
Computational complexity:
\(\displaystyle O(n^{2})\).