Instead of just calculating the hash of a sequence, we can store the value at each of its prefixes. Note that these will be hash values for sequences equal to the corresponding prefix.
With such a structure, you can quickly calculate the hash value for any subsegment of this sequence (similar to prefix sums).
If we want to calculate the hash of the subsegment [l;r], then we need to take the hash on the prefix r and subtract the hash on the prefix l-1 multiplied by p to the power of r-l+1. Why this is so becomes clear if you write the values on prefixes and see what happens. I hope you succeed looking at this picture.
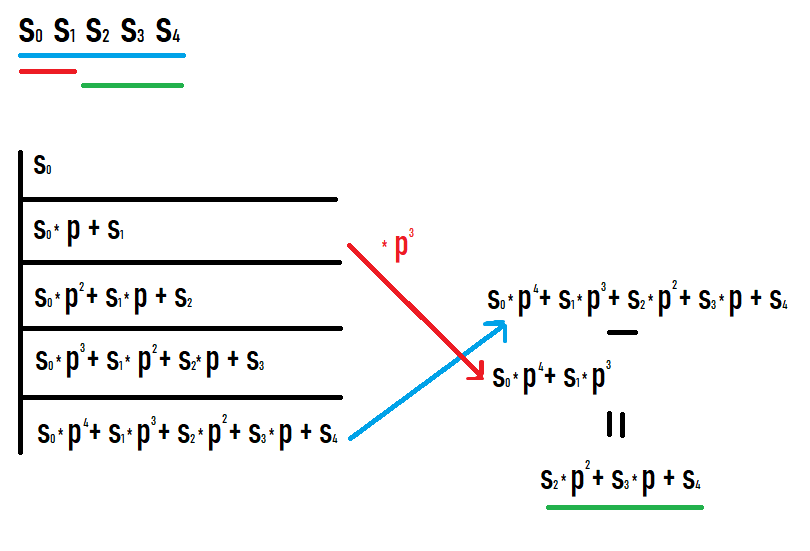
As a result of such actions, we get a hash of a subsegment of the original sequence. Moreover, this hash is equal to that if it were considered as a hash from a sequence equal to this subsegment (no additional conversions of degrees or the like are required to compare with other values).
There are two points to be clarified here:
1) To quickly multiply by p to the power r-l+1, it is necessary to precalculate all possible powers of p modulo mod.
2) It must be remembered that we perform all calculations modulo modulo, and therefore it may turn out that after subtracting the prefix hashes, we will get a negative number. To avoid this, you can always add mod before subtracting. Also, do not forget to take the modulo value after multiplications and all additions.
In code it looks like this:
#include <bits/stdc++.h>
using namespace std;
typedef long longll;
const int MAXN = 1000003;
// base and hash module
ll p, mod;
// prefix hash and exponents p
h[MAXN], pows[MAXN];
// calculating the hash of the subsegment [l;r]
ll get_segment_hash(int l, int r) {
return (h[r] + mod - h[l - 1] * pows[r - l + 1] % mod) % mod;
}
int main()
{
// somehow get p and mod
// precalculate powers p
pows[0] = 1;
for (int i = 0; i < MAXN; i++)
pows[i] = (pows[i - 1] * p) % mod;
//
// main problem solution
//
return 0;
}