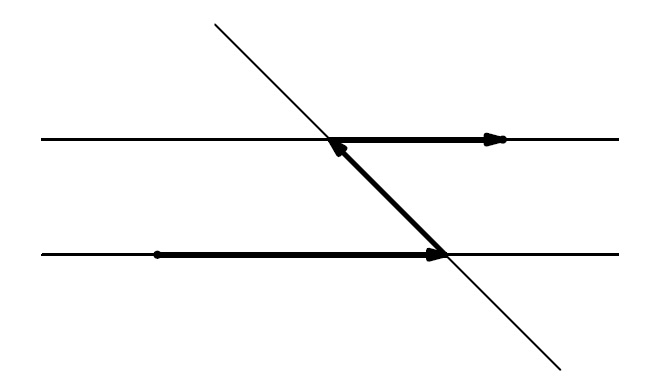
Problem
Petya and Vasya — Good friends. Therefore, they often visit each other. Recently Petya
got a driver's license and is going to visit his friend. For simplicity, we will assume that
all the roads in the city they live in are endless straight lines. At the intersection
two or more roads are crossroads. The houses of Petya and Vasya are located near some
city roads, but not at intersections.
Petya starts his journey on the road near his house. At the same time, he can choose any of the
two directions. When Petya approaches the intersection, he can turn to any other
the road passing through it or continue to drive along the current one. Since Petya is not very good
an experienced driver, every turn he makes makes him worry. And
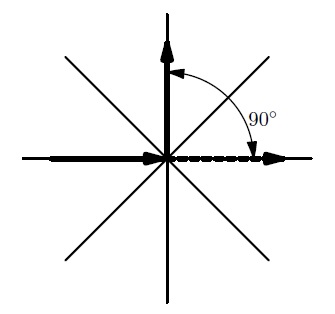
Petya's excitement is equal to the angle by which he turns, in degrees. For example, with
Petya's excitement at a right angle is 90.
With a less sharp turn, Petya worries less, and with a steeper — stronger.

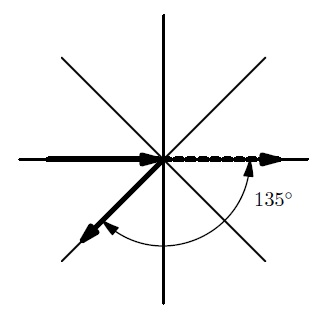
We will assume that Petya's excitement throughout the entire route is equal to the sum of the values in
degrees of angles that he will have to turn during the movement. Of course, Petya wants
take a route that will make him worry as little as possible.
Help Petya find out what is the minimum total excitement that he will experience,
having reached Vasya's house.
Input data format
The first line of the input file contains an integer n (1 ≤ n ≤ 50) — number of roads in
city. The next n lines contain the description of the roads.
Each road is described by four integers x1, y1, x2, y2, which are given by coordinates
two different points (x1, y1) and (x2, y2) through which the road passes.
It is guaranteed that no two roads are the same. The next two lines contain
coordinates of Petya and Vasya's houses. It is guaranteed that each house is on exactly one road,
and also that Petya and Vasya live in different places.
The coordinates of all points in the input file are integers and do not exceed 100 by
absolute value.
Output format
In the output file print a single number — the total angle, in degrees, by which
Petya will have to turn with the optimal choice of route. The answer is considered correct if
its relative or absolute error does not exceed 10−9.
If Petya can't get to Vasya's house, print the number −1.
Input
3
0 0 2 0
1 1 0 2
1 2 3 2
-3 0
3 2
Conclusion
270.0
Input
1
0 0 2 0
0 0
20
Conclusion
0.0
Input
5
0 0 1 0
0 0 1 1
0 0 0 1
0 0 -1 1
0 1 1 1
50
05
Conclusion
90.0
The following figure corresponds to the first example. Petya makes two 135 turns
degrees, its total wave is 270.