Combinations of n elements by k are compounds that can be formed from n elements, collecting k elements in each connection; while the connections differ from each other only by the elements themselves (the difference in the order of their arrangement is not taken into account).
For example, the following combinations can be formed from 3 elements (a,b,c)(a,b,c) 2 each: ab,ac,bc.
The number of all possible combinations that can be formed from n elements by k is indicated by the symbol

and calculated by the formula:
There are two ways to find the number of combinations

1. Find n!, k!, (n – k)! and according to the formula above, we calculate the quantity, but from – due to possible overflow, this method can be used with n <= 12.
2. With dynamic programming.
The DP will look like Pascal's triangle, with ones at the top and edges, and each number equals the sum of the two numbers above it.
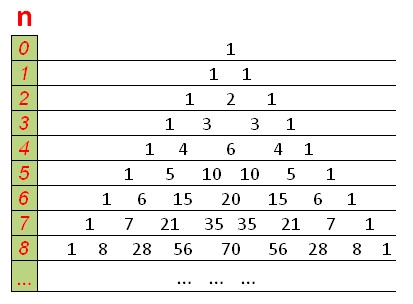
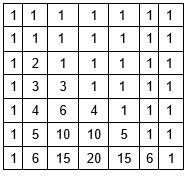
A function that counts the number of combinations using dynamic programming in O(n ^2 ):
int C(int n, int k)
{
vector<vector<int> > dp(n + 1, vector<int>(n + 1, 1)); // Create a dp array of size (n + 1, n + 1)
for (int i = 0; i <= n; i++) // Fill in the i-th line of the array
{
for (int j = 1; j < i; j++)
{
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; //recalculating (i;j) position through (i - 1; j - 1) and (i - 1; j)
}
}
return dp[n][k]; //return value
}