Problem
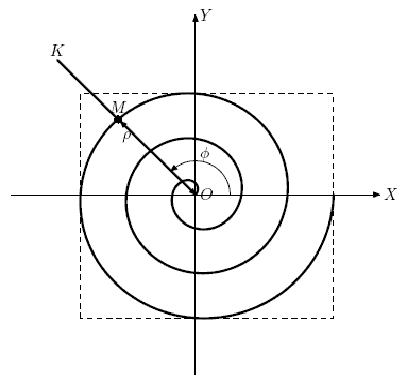
Dima recently joined the Research Institute of Flat Curves. As the name of this research institute suggests, it is engaged in various research in the field of plane curves. Recently, Dimin's boss Georgy encountered a very interesting curve, which, as it turned out after some research, is known as the Archimedean spiral. The Archimedean spiral is a plane curve depicting the trajectory of the point M, which moves uniformly along the ray OK with the origin at O, while the ray OK itself rotates uniformly around the point O (see figure). In other words, the distance to the origin ρ = OM linearly dependent on the angle of rotation .phi. beam OK. In this case, the rotation of the ray OK by the same angle corresponds to the same distance increment ρ.
The movement of point M can be set using a number of parameters:
• initial angle of rotation .alpha. beam OK (measured in degrees counterclockwise relative to the positive direction of the OX axis);
• angular velocity .omega. ray OK (measured in degrees per time unit);
• the initial distance R from point M to the origin (point O);
• velocity V of point M along the ray OK.
If, by setting these parameters, we do not limit the time of movement of the point M, then we get an infinite curve, which is quite difficult to explore. Therefore, Dima decided to confine himself to studying some part of this curve, the one that is obtained when the point M moves from the zero moment of time to the moment of time T. The problem that Dima solves is to find a rectangle of the minimum area with sides parallel to the coordinate axes, in which it can be inscribed.
You need to write a program that will find the desired rectangle
Input
The input file contains four integers: ω (1 ≤ omega; ≤ 100), V (1 ≤ V ≤ 100), R (0 ≤ R ≤ 100) and T (1 ≤ T ≤ 1000). In this problem, it is assumed that the initial rotation angle .alpha. is zero.
Output
In the first line of the output file print two real numbers — the coordinates of the lower left corner of the desired rectangle, and in the second line — coordinates of the upper right corner of the desired rectangle.
The answer will be considered correct if the value of each of the coordinates differs from the true value by no more than 10-5.
| Input |
Output |
| 60 10 0 18 |
-150.3028434716 -165.2754877824
180.0000000000 135.3362037333
|
Team Olympiad, VKOSHP, 2008, Problem I