Problem
A spider and a spider float on the lake on two branches. They can't swim, so they can only meet when the branches touch.
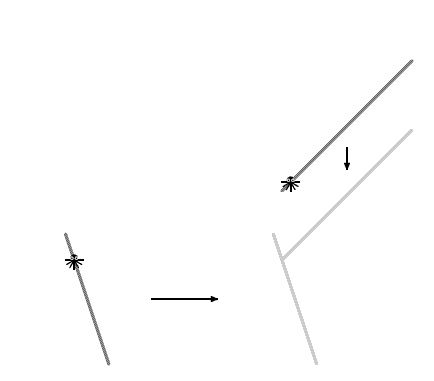
Assuming that branches are in the form of segments, and that they swim at constant speeds, determine how long it takes to meet the unfortunate arthropod.
Input
The input file contains 12 numbers: x1, y1, x2, y2, x 3, y3, x4, y4, v1x, v 1y, v2x, v2y. The coordinates of the vertices of the first segment: (x1, y1) and (x2, y2), coordinates vertices of the second segment: (x3, y3) and (x4, y4), the speed of the first segment (v1x, v1y), speed of the second segment (v2x, v2y). All numbers are integers and do not exceed 104 in absolute value. At the initial moment of time, the branches do not touch. Branches are guaranteed to have a non-zero length.
Output
Output in the output file the time until the nearest moment when the branches touch, with an error of no more than 10
−4. If the branches never touch, print the number -1.
| Input |
Output |
|
0 0 -1 3
4 4 7 7
3 0
0 -1
|
1.6 |
|
0 0 -1 3
4 4 7 7
10
0 -3
|
-1 |
Team Olympiads, St. Petersburg Schoolchildren Team Programming Championships, 2006, Problem E