Intersection of many

ID 38308. Advertising

Error

ID 38310. Transplants

On Novy Prospekt for unloading, it was decided to launch two new bus routes on different sections of the avenue.  The final stops of each of the buses are known. Determine the number of stops  where you can transfer from one bus to another.

Input
Four numbers are entered, not exceeding 100, specifying the numbers of the final stops. First for the first, then the second bus (see examples and picture).

Imprint
Your program should output a single number – desired number of stops.

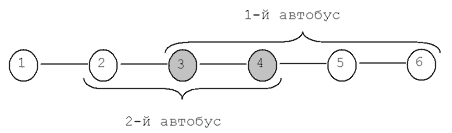
Examples

ID 38991. Advertising 2

The supermarket decided to broadcast advertisements for new products from time to time. In order to create the optimal schedule for broadcasting advertising, the supermarket management conducted the following study: during the day, for each customer who visited the supermarket, the time when he arrived at the supermarket and when he left it was recorded.

The advertising manager assumed that such a schedule of arrivals and departures of buyers would continue in the following days. He wants to schedule commercials so that each customer hears at least two advertisements. At the same time, he stipulated that two advertisements should not be broadcast at the same time and, since the sellers had to listen to these advertisements all the time, the total number of advertisements per day was minimal.

Write a program that will create such a schedule for broadcasting commercials. Advertisements can start broadcasting only at whole points in time. Each advertisement is considered to end before the next integer point in time. If an advertisement is broadcast at the moment when the customer enters or leaves the supermarket, the customer has time to hear this advertisement.

Input
The input file contains first the number N — number of shoppers visiting the supermarket per day (1<N<3000). Then comes N pairs of natural numbers Ai, Bi, specifying the time of arrival and departure of customers from the supermarket, respectively (0<A_i<B_i<106).

Imprint
In the output file, first print the number of advertisements that will be broadcast per day. Then output in ascending order the time points at which you want to broadcast advertisements.

If there are several solutions, print any of them.
 

Examples

ID 43772. Triangle of Maxim

Since childhood, Maxim was a good musician and jack of all trades. Recently, he independently made a simple percussion musical instrument — triangle. He needs to know what the frequency of the sound his instrument is making.

Maxim has a professional music tuner with which you can play a note at a given frequency. Maxim acts as follows: he turns on notes with different frequencies on the tuner and for each note determines by ear whether it is closer or further to the sound emitted by the triangle than the previous note. Since Maxim's hearing is absolute, he always determines this absolutely correctly.

Maxim showed you a recording in which the sequence of frequencies set by him on the tuner is given, and about each note, starting from the second, — closer or further it is to the sound of the triangle than the previous note. It is known in advance that the sound frequency of the Maxim triangle is not less than 30 hertz and not more than 4000 hertz.

It is required to write a program that determines in what interval the frequency of the sound of a triangle can be.

Input
The first line of the input file contains the integer n — the number of notes played by Maxim using the tuner (2 ≤ n ≤ 1000). The next n lines contain Maxim's entries, and each line contains two components: a real number f_i — the frequency set on the tuner, in hertz (30 ≤ f_i ≤ 4000), and the word "closer" or the word "further" for every frequency except the first one.

The word "closer" means that the frequency of this note is closer to the frequency of the triangle than the frequency of the previous note, which is formally described by the relationship: |f_i−f_triangle.| < |f_i−1−f_triangle|

The word "further" means that the frequency of this note is further than the previous one.

If it turned out that the next note is as close to the sound of a triangle as the previous note, then Maxim could write down any of the two words mentioned above.

It is guaranteed that the results obtained by Maxim are consistent.

Imprint
In the output file, you need to output two space-separated real numbers — the smallest and the largest possible value of the sounding frequency of the triangle made by Maxim. Numbers must be printed with a precision of at least 10⁻⁶.

 

Examples

ID 38583. Two buttons

Alice and Bob control the robot. Each of them has one button that controls the robot. Alice started holding the button A seconds after starting the robot and released the button  B seconds after trigger. Bob started holding the button C seconds after trigger and released the button after D seconds after trigger.  How many seconds did Alice and Bob hold their buttons at the same time?

Input
Input 4 integers: A, B, C and D (\(1<=A<B<=100\), \(1<=C<D<=100\) ).

Imprint
Print the length of time (in seconds) that Alice and Bob held their buttons simultaneously.
 

Examples

ID 37669. Metro

At some cross-platform metro stations (like Tretyakovskaya, for example), trains from different directions come to different sides of the platform. Tanya agreed to meet her friend at such a station, but since her friend arrived from another time zone, she overslept because of the jet lag, and Tanya had to wait a long time for her. Trains always run exactly on schedule, and Tanya knows that the train stops on the platform for exactly one minute, and the interval between trains (the time when there is no train at the platform) is a minutes for trains on the first track and b  minutes for trains on the second track. That is, a train arrives on the first track and stops for one minute, then for a minutes there is no train at the platform, then for one minute the next train stops at the platform, etc.

While Tanya was standing on the platform, she counted n trains on the first track and m trains on the second track. Determine the minimum and maximum time that Tanya could spend on the platform, or report that she definitely lost count.

All the trains that Tanya saw, she watched for the whole minute, that is, Tanya does not come and go from the platform in the middle of the minute when the train is on the platform.

Input
The first line of the input contains a number a - the interval between trains on the first track. The second line contains the number b - the interval between trains on the second track. The third line contains the number n - the number of trains on the first track that Tanya saw. Fourth line
contains the number m - the number of trains on the second track that Tanya saw. All numbers are integers,
from 1 to 1000.

Imprint
The program should display two numbers: the minimum and maximum time in minutes that Tanya could stand on the platform, or one number -1 if Tanya was definitely mistaken.
 

ID 37669. Metro

At some cross-platform metro stations (like Tretyakovskaya, for example), trains from different directions come to different sides of the platform. Tanya agreed to meet her friend at such a station, but since her friend arrived from another time zone, she overslept because of the jet lag, and Tanya had to wait a long time for her. Trains always run exactly on schedule, and Tanya knows that the train stops on the platform for exactly one minute, and the interval between trains (the time when there is no train at the platform) is a minutes for trains on the first track and b  minutes for trains on the second track. That is, a train arrives on the first track and stops for one minute, then for a minutes there is no train at the platform, then for one minute the next train stops at the platform, etc.

While Tanya was standing on the platform, she counted n trains on the first track and m trains on the second track. Determine the minimum and maximum time that Tanya could spend on the platform, or report that she definitely lost count.

All the trains that Tanya saw, she watched for the whole minute, that is, Tanya does not come and go from the platform in the middle of the minute when the train is on the platform.

Input
The first line of the input contains a number a - the interval between trains on the first track. The second line contains the number b - the interval between trains on the second track. The third line contains the number n - the number of trains on the first track that Tanya saw. Fourth line
contains the number m - the number of trains on the second track that Tanya saw. All numbers are integers,
from 1 to 1000.

Imprint
The program should display two numbers: the minimum and maximum time in minutes that Tanya could stand on the platform, or one number -1 if Tanya was definitely mistaken.