| Problem description | | Progress |
|
Темы:
Arrays
Prefix sums(minimums, ...)
Dynamic Programming: One Parameter
We have a grid with H rows and W columns. The square in the ith row and jth column will be called Square(i, j). Integers from 1 to H·W are written over the entire grid, and an integer written in Square(i, j) is equal to Ai,j.
You are a wizard and can teleport a shape placed on Square(i, j) to Square(x, y) by spending \(|x-i|+|y-j|\) magiks (magic coins).
Now you need to pass Q practice tests on your abilities as a wizard (sorceress). Ith test will be conducted as follows:
- initially the figure is located in the square, where the integer is written Li;
- Let x be the integer written in the square occupied by the shape. Repeatedly move the shape to the square where the integer x+D is written until x will not become equal to Ri. The test ends when x = Ri .
It is guaranteed that Ri- Li is divisible by D.
For each test, find the sum of magics consumed during that test.
Input
The first line contains three integers: H, W and D (\( 1\leq H,W \leq 300\), \(1 \leq D \leq H \cdot W\)).
The following H lines contain W numbers Ai,j (\(1 \leq A_{i,j} \leq H \cdot W\), \(A_{i,j} \ neq A_{x,y} ((i,j) \neq (x,y))\).
The next line contains an integer Q (\(1 \leq Q \leq 10^5\)).
The last Q lines contain 2 integers each: Li and Ri (\(1 \leq L_i \leq R_i \leq H \cdot W\)), \((R_i-L_i)\) multiple of D.
Imprint
For each test, print the sum of magics spent during this test. The output should be in the order of the tests.
Examples
| # |
Input |
Output |
Explanations |
| 1 |
3 3 2
1 4 3
2 5 7
8 9 6
1
48 |
5 |
- 4 is written as Square(1,2).
- 6 is in Square(3,3).
- 8 is written in Square (3,1).
Thus, the sum of magic points spent during one test is:
\((|3-1|+|3-2|)+(|3-3|+|1-3|)=5\).
|
| 2 |
4 2 3
37
14
5 2
68
2
2 2
2 2 |
0
0 |
Note that there may be a test where the shape doesn't move at all, and there may be multiple identical tests. |
| 3 |
5 5 4
13 25 7 15 17
16 22 20 2 9
14 11 12 1 19
10 6 23 8 18
3 21 5 24 4
3
13 13
2 10
13 13
| 0
5
0 |
|
| |
![]()
|
|
Темы:
Arrays
Processing algorithms
Gromozek has a sequence of integers A of length N. It will make three slices in the A sequence and split it into four (non-empty) contiguous subsequences B, C, D > and E. He chooses the positions of the slices arbitrarily. Let P, Q, R, S be the sums of elements in B, < code>C, D, E respectively. Gromozeka will be happy when the absolute difference between the maximum and minimum between P, Q, R, S minimum. Find the smallest possible absolute difference between the maximum and minimum between P, Q, R, S.
Input
The first line contains an integer N (\(1<=N<=2 \cdot 10^5\)). The second line contains N integers Ai (\(1<=A_i<=10 ^9\)).
Imprint
Print the smallest possible absolute difference between the maximum and minimum between P, Q, R, S.
Examples
| # |
Input |
Output |
Explanations |
| 1 |
5
3 2 4 1 2
| 2 |
If we divide A by B, C, D, E = (3), (2), (4), (1,2), then P = 3, Q = 2, R = 4, S = 1 + 2 = 3.
Here the maximum and minimum among P, Q, R, S are 4 and 2, with an absolute difference of 2.
We can't make the absolute difference between the maximum and minimum less than 2, so the answer is 2. |
| 2 |
10
10 71 84 33 6 47 23 25 52 64
| 36 |
|
| 3 |
7
1 2 3 1000000000 4 5 6
| 999999994 |
|
| |
![]()
|
|
Темы:
Cycles
Arrays
Gromozeka has the following two personal principles: he never travels more than L in one day. He never sleeps outdoors. That is, he must be at the hotel at the end of the day.
The Planet Blue has N hotels and all are located on the same street. The coordinate of the ith hotel (1<=i<=N) is xi.
Traveling around the planet Bluk, Gromozeka planned Q moves. With each move he plans to change hotel aj to bj (1<=j<= Q). For each move, find the minimum number of days Gromozeka needs to get from the ajth hotel to the bjth, following his principles.
It is guaranteed that he can always travel from the ajth hotel to the bjth th hotel.< br />
Input
The first line contains an integer N (2<=N<=105) - the number of hotels on the planet Bluk. The second line contains N numbers xi - coordinates of the i-th hotel (1<=x1<x2< /sub><...<xN<=109 , xi+1−x i<=L). The third line contains the number L (1<=L<=109). The fourth line contains the number Q (1<=N<=105).
The last Q lines contain two different numbers aj and bj (1<=aj,bj<=N). All numbers are integers.
Imprint
Print Q lines. The j-th line (1<=j<=Q) should contain the minimum number of days Gromozeka needs to get from aj-th hotel to bj-th hotel.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
9
1 3 6 13 15 18 19 29 31
10
4
18
7 3
67
8 5 |
4
2
1
2 |
On the 1st crossing, he can travel from the 1st hotel to the 8th in 4 days as follows:
Day 1: Transfer from the 1st hotel to the 2nd hotel. Distance traveled - 2.
Day 2: Transfer from the 2nd hotel to the 4th. Distance traveled - 10.
Day 3: Transfer from the 4th hotel to the 7th. Distance traveled - 6.
Day 4: Transfer from the 7th hotel to the 8th. Distance traveled - 10. |
| |
![]()
|
|
Темы:
Cycles
Arrays
In some world, it's December 31st and all the fun is just beginning. Snezhik Sugrobovich made N large snowballs and arranged them in a row from left to right. On each ith snowball, counting from the left (1 <= i <= N ), he wrote the integer ai. He invites you to play a game. Snezhik Sugrobovich allowed to break no more than N − 1 snowballs of your choice.
Let's say there are K snowballs left. Snezhik Sugrobovich will be satisfied and give you a good gift if for each integer i (1<=i<=K) on the i-th snowball, counting the remaining snowballs on the left , an integer will be written i.
Find the minimum number of snowballs you need to break in order to receive a gift. If it doesn't work, then print -1.
Input
In the first line, the program receives an integer N (1 <= N <= 200000) as input. In the second line - N natural numbers ai (1<=ai<=N).
Imprint
Print the minimum number of snowballs that need to be broken to get a present, or print -1 if it's impossible.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
3
2 1 2
| 1 |
Break the first snowball, the numbers on the rest of the snowballs will satisfy Snezhik Sugrobovich's condition |
| 2 |
3
2 2 2
| -1 |
|
| 3 |
10
3 1 4 1 5 9 2 6 5 3
| 7 |
|
| 4 |
1
1 |
0 |
|
| |
![]()
|
|
Темы:
Arrays
Create a vector and fill it with positive elements only.
Input
The first line is the number of elements in the array. The second line contains the elements of the array.
Output
Output only positive elements from the sequence.
Examples
| # |
Input |
Output |
| 1 |
4
2 -4 0 100
| 2 100 |
| |
![]()
|
|
Темы:
Arrays
You are given a sequence of integers. Write a program that creates and sorts an array in descending order.
Input
First given number N — the number of elements in the array (1<=N<=100). Then N numbers are written separated by a space - elements of the array. The array consists of integers.
Output
It is necessary to output an array sorted in descending order.
Examples
| # |
Input |
Output |
| 1 |
5
4 56 23 67 100
| 100 67 56 23 4 |
| |
![]()
|
|
Темы:
Arrays
Processing algorithms
Given two integer sequences, each of length N: A = (A1, A 2, ..., AN) and B = (B1, B2, ..., BN).
All A elements are different. All B elements are also different.
Print the following two values.
- The number of integers contained in both
A and B appearing in the same position in the two sequences. In other words, the number of integers i numbers such that Ai = Bi.
- The number of integers contained in both
A and B that appear at different positions in the two sequences. In other words, the number of pairs of integers (i, j) numbers such that Ai = Bj and i ≠ j.
Input
The program receives three lines as input. The first line contains one number N (1 <= N <= 1000) - the number of numbers in the sequence. The second line contains numbers A1, A2, ..., AN, all numbers are different . The third line contains numbers B1, B2, ..., BN , all numbers various (1 <= Ai, Bi <= 109).
Imprint
Print the answer to the first question on the first line, and the answer to the second on the second line.
Examples
| # |
Input |
Output |
| 1 |
4
1 3 5 2
2 3 1 4
|
1
2
|
| 2 |
3
1 2 3
4 5 6
|
0
0
|
| |
![]()
|
|
Темы:
2D arrays
Arrays
On a chessboard of N x times; There are N rooks in chess that do not attack each other, that is, there is exactly one rook on each vertical and each horizontal.
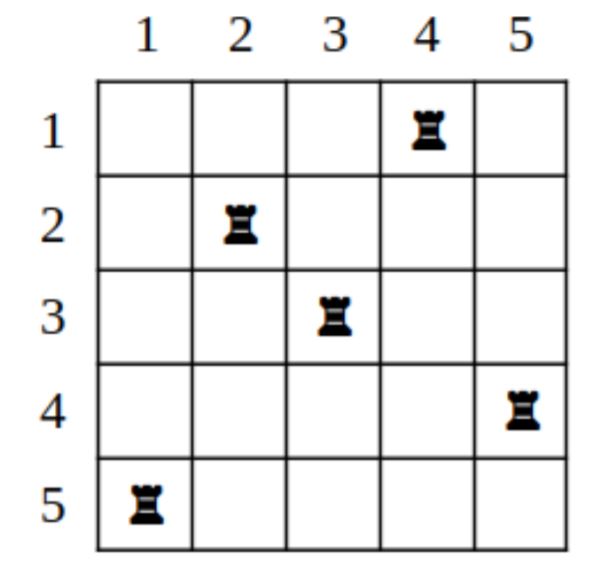
The chessboard is rotated 90° clockwise. Output the resulting set-up of rooks.
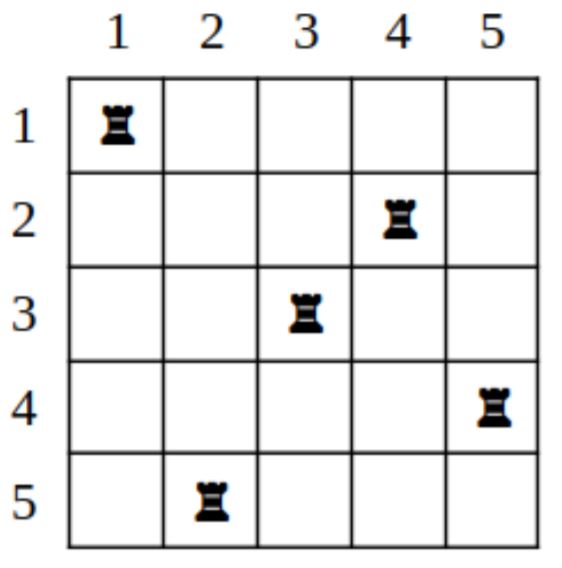
Input
The first line of the input contains an integer N, 1 ≤ N≤ 105 — board size. The next N lines contain one number each from 1 to N, namely, the i-th line contains the number ai — number of the column in which the rook stands on the i-th column. In this problem, the horizontals are numbered from 1 to N from top to bottom, the verticals are numbered from 1 to N from left to right (see figure).
Imprint
The program should output N numbers — the placement of the rooks after the turn in the same format.
Examples
| # |
Input |
Output |
| 1 |
5
4
2
3
5
1 |
1
4
3
5
2 |
Remark
The example in the condition corresponds to the figures. Initially, the rooks stood in columns 4, 2, 3, 5, 1
when listing them line by line from top to bottom. After turning, the rooks are in columns 1, 4, 3, 5, 2.
| |
![]()
|