| Problem description | | Progress |
|
Темы:
Bust
In my hallway there are 20 slippers in a row – 10 left and 10 right. Coming home, I change my shoes and choose two slippers – left and right, in which it is most convenient for me to stick my legs. Naturally, the left slipper should be to the left of the right one, and the distance (number of other slippers) between them should be as small as possible. Write a program that calculates how many slippers are between the ones I feel most comfortable wearing.
Input
A sequence of 10 zeros and 10 ones is entered, written in some order. The unit corresponds to the left slipper, 0 – right slipper. Numbers are separated by spaces.
Imprint
The program should print the number of slippers between the most comfortable slippers, or -1 if there are none.
Examples
| # |
Input |
Output |
| 1 |
1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 |
0 |
| |
![]()
|
|
Темы:
Conditional operator
One-Dimensional Arrays
date and time
Bust
The alarm clock on a cell phone can be set to ring at the same time every day, or at a specified time on a specific day of the week. Multiple alarms can be set independently.
Use the information about alarms and the current time and day of the week to determine when the next alarm will sound.
Input
The first line contains three numbers that specify the current time: the day of the week (from 1 to 7), hours and minutes.
The second line contains one natural number N, not exceeding 100 – number of alarms.
The next N lines contain descriptions of N alarm clocks. The description of each alarm consists of three numbers: day of the week (a number from 1 to 7 for Monday, …, Sunday, respectively, 0 – if the alarm should ring every day), hours (from 0 to 23), minutes (from 0 to 59).
Imprint
Print separated by a space, three numbers specifying the day of the week, hours and minutes when the next alarm clock rings.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
2 10 20
2
1 23 15
0 10 10
| 3 10 10 |
|
| 2 |
7 1 1
3
7059
7 23 59
7 1 1
| 7 1 1 |
In the second example, the third alarm will ring at the start time. |
| |
![]()
|
|
Темы:
Strings
Bust
Several letters (possibly repeating) are written around the circle. Petya wonders if he will be able to read a certain word if he moves in a circle (in any direction) without missing letters (he can choose where to start and in which direction to move).
Input
The first line contains lowercase Latin letters in the order in which they are arranged in a circle clockwise. Letters are written without spaces, their number is not less than 1 and not more than 100.
The second line contains the word Petya wants to find. It also consists of lowercase Latin letters and has a length from 1 to 100.
Imprint
Print YES in capital Latin letters if such a word can be read moving in a circle, and NO otherwise.
Examples
| # |
Input |
Output |
| 1 |
abcdefg
abd |
NO |
| 2 |
abcdg
bag |
YES |
| 3 |
a
aaa |
YES |
| |
![]()
|
|
Темы:
Cycles
Bust
In some card game, a deck is used, in which there are 4 aces. 4 players take part in the game, each of which is dealt an equal number of cards, and two cards are put aside.
Each player boasted how many aces he had. Determine how many players knowingly lied.
For example, they said 1, 1, 1, 2. Therefore, 1 player obviously lied. (Some three could tell the truth, but all four could not tell the truth, since there are only 4 aces).
Input
4 numbers are entered (from 0 to 9 each), separated by a space – the number of aces according to the first, second, third and fourth players.
Imprint
Print one number – the minimum number of players who knowingly lied. If everyone could tell the truth at the same time, print the number 0.
Examples
| # |
Input |
Output |
| 1 |
1 1 1 2 |
1 |
| 2 |
1 1 1 1 |
0 |
| |
![]()
|
|
Темы:
Bust
recursion
Two-pan balances and a set of weights are given. An object weighing K grams is placed on the left side of the scale. Is it possible to bring the scales to a state of equilibrium, and if so, determine for each scale pan which weights need to be placed on it for this. Available weights are allowed to be placed on any of the scales (each weight is available only in one copy, some weights may not be used).
Input
Entered first K — the weight of the item placed on the left bowl (1≤K≤50). Next, the total number of weights N (1≤N≤10) is recorded. Next, N different natural numbers are written, not exceeding 50, — weights.
Imprint
On the first line print the weights of the weights to be placed on the left scale pan, on the second line print — weights to be placed on the right bowl. If no weights need to be placed on some bowl — print the number 0 in this line. If it is impossible to balance the scales with the help of these weights, print the single number –1. If there are several options, print any of them.
Examples
| # |
Input |
Output |
| 1 |
5
2
3 5
| 0
5 |
| 2 |
5
3
6 3 4
| 4
36 |
| 3 |
5
1
2 |
-1 |
| |
![]()
|
|
Темы:
Bust
On a tropical island, kvass is especially popular at the height of the tourist season. Previously, all kvass was imported from Russia, but with the increasing popularity of this drink, the question arose of producing kvass right on the spot. There are N resort towns on the island, all towns are located on the coast. The only ring road on the island runs along the coast, connecting all the cities. Driving on the road is possible in any direction. Each city knows how many barrels of kvass it needs daily.
It is planned to build only one plant in any city, and deliver products to other cities. Transportation of one barrel to a neighboring city costs one tugrik (local currency).
Your task is to determine in which city the factory should be built in order to minimize transport costs.
Input
The first line of the input contains the number N – number of cities (N ≤ 10) and N numbers – the amount of kvass required daily by the 1st, 2nd, …, Nth city (the cities are numbered consecutively along the ring road).
Imprint
Print one number – the number of the city in which the factory should be built. If there are several suitable cities – print the number of any of them.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
3 5 3 10 |
3 |
|
| 2 |
6 4 4 1 5 1 3 |
2 |
There are 6 cities on the island, the need for each city is indicated in circles, the city number is next to the circle.
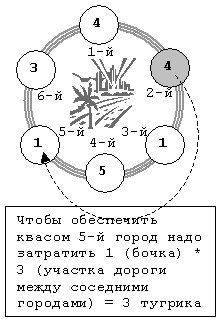
If you build a plant in the 2nd city (it is grayed out), you will need to pay 4 + 1 (the cost of transportation to the 1st and 3rd cities) + 5*2 + 3*2 (to the 4th and 6th ) + 1*3 (in the 5th, see the picture).
In the 2nd we do not carry anything at all. It will be 24 tugriks. It is easy to check that if you build a plant in other cities, the amount will be higher. For example, if you build in the 4th city, then the sum will be 1 + 1 + 3*2 + 4*2 + 4*3 = 28 tugriks. |
| |
![]()
|
|
Темы:
Simple puzzles
Bust
Petya has a playing field of 3x3 size, filled with numbers from 1 to 9. At the beginning of the game, he can place a chip in any cell of the field. At each step of the game, it is allowed to move a piece to any cell adjacent to the side, but it is not allowed to visit the same cell twice. Petya carefully keeps the protocol of the game, writing down the numbers in it in the order in which the chip visited the cells. Petya was wondering what is the maximum number he can get in the protocol. Help him answer this question.
Input
The input file contains the description of the — 3 lines of 3 integers separated by spaces. It is guaranteed that all nine numbers are different and lie in the range from 1 to 9.
Imprint
Print a single integer — the maximum number that could result in the protocol when playing on this field.
The answer can be displayed not as a number, but as a string or as a sequence of individual digits (but not separated by spaces).
Examples
| # |
Input |
Output |
| 1 |
1 2 3
4 5 6
7 8 9
| 987456321 |
| |
![]()
|
|
Темы:
Bust
Partitions
In football tactics, one of the basic concepts is the game scheme. It determines how many of the ten outfield players will play defense, how many — in midfield and how much — on the attack.
For example, a 5-3-2 formation means a team has five defenders, three midfielders, and two forwards. In accordance with modern concepts, the following restrictions are imposed on the game scheme: there must be at least one and no more than five defenders, at least one and no more than five midfielders and no more than three attackers. Note that the attackers may not be in the team at all. We will consider only such schemes.
We will assume that the football field has a length of 120 meters and a width of 80 meters. Let us introduce a rectangular Cartesian coordinate system on it in such a way as shown in the figure. The gates of the team we are considering are on the left.
We will also assume that a player is in the midfield line at some point in time if he is at a distance of no more than 20 meters from the center line. Accordingly, the player is in the line of defense if he is no more than 40 meters from "his" the front line, and in the attack line, if it is located no more than 40 meters from the "stranger" front line.
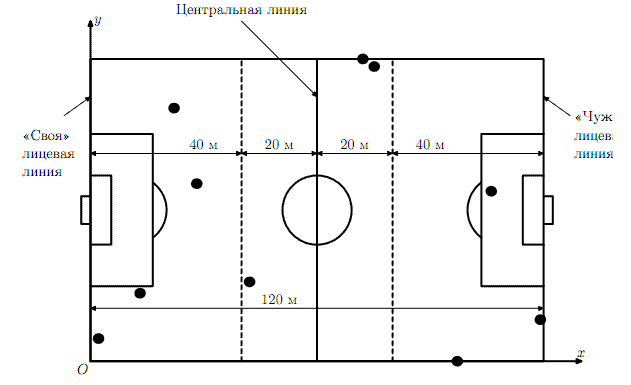
For example, in the situation shown in the figure, there are four players in the defensive line, in the midfield line — three, in the line of attack — also three.
During the game, some players can move from one line to another. In this problem, we assume that it is possible to move from midfield to defense (and vice versa) and from midfield to attack (and vice versa). Thus, a player who, in accordance with the scheme of the game, is a defender, cannot be in the offensive line, and vice versa — a player who, according to the scheme of the game, is an attacker, cannot be in the defensive line. In addition, in accordance with the instructions of the coach, no more than two players could move from each line to each.
Your task is to write a program that, given the positions of the players at some point in time, will find all possible game schemes under which such an arrangement of players could arise during the game.
Input
The input file contains ten lines containing two integers xi and yi each, — coordinates of each player on the team (0 ≤ xi ≤ 120, xi ≠ 40, xi ≠ 80, 0 &le ;yi ≤80).
Imprint
In the first line of the output file print k — the number of game formations a team can play. On the next k lines, in any order, print a description of each of these schemes. Follow the data format shown in the example.
Examples
| # |
Input |
Output |
| 1 |
97 0
13 18
26
119 11
42 21
72 80
75 78
106 45
22 67
28 47 |
9
2-5-3
3-5-2
3-4-3
4-5-1
4-4-2
4-3-3
5-4-1
5-3-2
5-2-3
|
| |
![]()
|
|
Темы:
Formula derivation
Bust
Farmer John has N spotted cows and N spotless cows. As a geneticist, FD is certain that the spots on his cows are caused by a mutation in the cow's genome.
For a lot of money, the FD issued the genomes of his cows. Each genome is a string of length M, consisting of four characters A, C, G, T. When he wrote out the genomes of all cows, he got the table below for N=3:
Position: 1 2 3 4 5 6 7 ... M
Spotted Cow 1: A A T C C C A ... T
Spotted Cow 2: G A T T G C A ... A
Spotted Cow 3: G G T C G C A ... A
Cow without spots 1: A C T C C C A ... G
Cow without spots 2: A G T T G C A ... T
Cow without spots 3: A G T T C C A ... T
Looking closely at this table, he suggested that positions 2 and 4 might be responsible for the spotting. Because by looking at the characters in these positions, the FD can predict which of his cows are spotted and which are not (for example, if he sees G and C, then the cow is not spotted).
FD suggested that it could be explained by a set of three different positions. Help him count the number of three different positions that could explain the spotting.
INPUT FORMAT:
The first input line contains NN (1≤N≤500) and MM (3≤M≤50). Each of the following N lines contains M characters. This is a description of the genomes of spotted cows. The next N lines describe the genomes of spotless cows.
OUTPUT FORMAT:
Compute the number of sets from three different positions that can explain the spotting. A plurality of three different positions can explain spotting if spotting can be predicted absolutely accurately for a population of FD cows by analyzing these three positions of the genome.
| Input |
Output |
|
3 8
ATCCCAT
GATTGCAA
GGTCGCAA
ACTCCAG
ACTCGCAT
ACTTCCAT
|
22 |
| |
![]()
|
|
Темы:
Depth walk
Bust
Implementation task
Farmer John is testing a new camera that can "grab the picture" and automatically calculate the position of the cows. Unfortunately, the camera does not have a very good algorithm for finding cows and the FD needs your help.
The picture taken by the camera can be described by a lattice of NxN characters, each in the range A…Z, representing one of 26 possible different colors. The FD considers the following cow recognition algorithm to be the best: PCL (possible placement of a cow) is a rectangle on a lattice (possibly the entire lattice) with sides parallel to the sides of the lattice, which does not contain other PCLs inside and has the following property: exactly two colors must be present inside this rectangle, one forms a continuous region and the other forms two or more continuous regions.
For example, this image
AAAAA
ABABA
AAABB
is PCL because the A characters form a contiguous region, the B characters form more than one contiguous region. The interpretation is a cow with color A and spots with color B.
A region is continuous if you can traverse the entire region by moving from one cell to another neighboring one in the directions up, down, left, right.
Based on the given image of the PD camera, determine the amount of PCL.
INPUT FORMAT:
The first line of input contains N, the size of the grid (1≤N≤20). The next N lines describe the image, each consisting of N characters.
OUTPUT FORMAT:
Amount of PCL in the image.
| Input |
Output |
|
4
ABBC
BBBC
AABB
ABBC
|
2 |
| |
![]()
|
|
Темы:
Formula derivation
Bust
Farmer John wants to create a triangular pasture for his cows.
There are N fence posts in total (3 ≤ N ≤ 100) as distinct (X1,Y1)…(XN, YN) points on the farm map. He can choose three of them to form the vertices of a triangular pasture, but so that one of the sides is parallel to the x-axis and the other is parallel to the y-axis.
What is the sum of the areas of all possible pastures that a FD can form?
Input
The first line contains N.
Each of the following N lines contains two integers Xi and Yi, each in the interval −104…104 inclusive, describing the position of the post.
Imprint
Since the sum of areas may not be an integer and very large, print the remainder after dividing twice the sum of areas by 109+7.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
4
0 0
0 1
10
1 2
|
3 |
Points (0,0), (1,0), (1,2) form a triangle with area 1.
Points (0,0), (1,0), (0,1) form a triangle with area 0.5.
So the answer is 2⋅(1+0.5)=3. |
| |
![]()
|
|
Темы:
Bust
meet in the middle
John's farm is represented by a grid of N×N fields (2≤N≤18), each labeled with a letter of the alphabet. For example,
ABCD
BXZX
CDXB
WCBA
Every day Besi the cow goes from the upper left corner to the lower right, moving either one cell to the right or one cell down. Besi writes down the string that results from her route, built from the letters she walked. She will be very upset if the resulting string turns out to be a palindrome (it reads the same from beginning to end and from end to beginning), because she will get confused in which direction she went.
Please help Besie figure out how many different palindromes she can form during her journey. Different ways to form the same palindrome should only be counted once. For example, in the example above, there are several ways to form the palindrome ABXZXBA, but there are only 4 different palindromes that Besi can form ABCDCBA, ABCWCBA, ABXZXBA, ABXDXBA.
INPUT FORMAT :
The first line of input contains N and subsequent N lines contain N< /strong> field description. Each line contains N characters in the range A..Z.
OUTPUT FORMAT :
Print the number of distinct palindromes Besi can form.
| Input |
Output |
|
4
ABCD
BXZX
CDXB
WCBA
|
4 |
| |
![]()
|
|
Темы:
Bust
Farmer John and Besi the cow love to trade math puzzles in their free time. The last puzzle FD gave to Besie was quite difficult and Besie couldn't solve it. Now she wants to give FD a very difficult puzzle.
Besi gives a FD expression (B+E+S+S+I+E)(G+O+E+S)(M+O+O), containing seven variables B,E, S,I,G,O,M ("O" is a variable, not 0). For each variable, it gives the FD a list of up to 20 integers that this variable can accept. Besi asks the FD to count the number of different ways to assign values to variables so that the calculated expression is an even number.
Input
The first line of input contains an integer N. Each of N the following lines contains a variable and a possible value for that variable. Each variable will appear in this list at least once and at most 20 times. For the same variable, all given values are different. All values range from −300 to 300.
Output
Print a single integer that specifies the number of ways the FD can assign values to variables in order for the expression to give an even result.
| Input |
Output |
10
B2
E 5
S7
I 10
O 16
M19
B3
G1
I 9
M2
|
6 |
There are 6 possible options for assigning values to variables:
(B,E,S,I,G,O,M) = (2, 5, 7, 10, 1, 16, 19) -> 53.244
= (2, 5, 7, 10, 1, 16, 2) -> 35.496
= (2, 5, 7, 9, 1, 16, 2) -> 34.510
= (3, 5, 7, 10, 1, 16, 2) -> 36.482
= (3, 5, 7, 9, 1, 16, 19) -> 53.244
= (3, 5, 7, 9, 1, 16, 2) -> 35.496
Note that (2,5,7,10,1,16,19) and (3,5,7,9,1,16,19) are treated as different assignments even though they give the same result.
| |
![]()
|
|
Темы:
Bust
Cows are addicted to word puzzles. For example, like this
USOPEN
OOMABO
MOOMXO
PQMROM
Like cows, they are only interested in the single word "MOO", which can appear in many places horizontally, vertically, or diagonally. The example above contains 6 such words.
Farmer John is also a fan of such puzzles. Because the cows don't want him to solve the puzzle before the cows, they encrypt the puzzle using a substitution cipher that replaces each letter of the alphabet with some different letter. For example, A can be replaced by the letter X, B by the letter A, and so on. No letter is replaced by itself, and no two letters are replaced by the same letter (otherwise the transcript may become ambiguous).
Unfortunately, the cows have lost their encryption table and are now unable to decipher their puzzle. Please help them determine the maximum number of MOO words that can exist for their puzzle by choosing the appropriate encryption table
INPUT FORMAT :
The first line of input contains N and M describing the number of rows and columns in the puzzle (both no more than 50). Each of the following N lines contains M characters describing one line of the encrypted puzzle. Each character is a capital latin letter in the range A..Z.
OUTPUT FORMAT :
Print the maximum possible number of MOO words contained in the puzzle, if it is decrypted with the appropriate encryption table.
| Input |
Output |
|
4 6
TAMHGI
MMQVWM
QMMQSM
HBQUMQ
|
6 |
Explanation
This is the puzzle given at the beginning of the problem, where "M" and "O" were replaced by "Q" and "M" respectively.
| |
![]()
|
|
Темы:
Bust
Strings
Little known is the fact that cows have their own alphabet "cowphabet". It consists of the same 26 letters from 'a' to 'z', but in a different order.
To pass the time, Besi mumbles cowphabet over and over again. Farmer John wonders how many times she's muttered it.
Given a string of letters that the FD heard from Besie's muttering, determine the minimum number of times Besie must mutter cowphabet for the FD to hear the given string. The FD doesn't always pay attention to Besie's mutterings, so he may not be able to hear some of the Besie's muttering letters. The string given to you contains only those letters that he heard.
Input
The first input line contains 26 small Latin letters from 'a' to 'z' in the order they appear in cowphabet. The next line contains a string of small Latin letters that the FD heard. This string has a length between 1 and 1000.
Imprint
Print the minimum number of times that Bessy muttered the alphabet.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
abcdefghijklmnopqrstuvwxyz
mood
|
3 |
In this example, cowphabet is ordered like a normal alphabet.
Bessie muttered cowphabet at least 3 times. Below is how Besi muttered, and in capital letters what letters FD heard.
abcdefghijklMnOpqrstuvwxyz abcdefghijklmnOpqrstuvwxyz abcDefghijklmnopqrstuvwxyz
|
| |
![]()
|
|
Темы:
Bust
Farmer John wants to take a picture of his grazing cows so he can hang it on his wall. The pasture is represented by a grid of N * N cells (like an NxN chessboard) (2≤N≤1000). The FD wants the cows to be distributed around the pasture with the following rules:
No two cows can be in the same cell.
Each sublattice of size 2×2 (total such sublattices are (N−1)×(N−1)) must contain exactly 2 cows
For example, this placement complies with the rules:
CCC
...
CCC
And such accommodation - no
C.C
.C.
C..
because the 2×2 region in the lower right contains only one cow.
There are no other restrictions. You can assume that the FD has an infinite number of cows.
Some cells are more preferable for PD than others. In particular, the FD considers. that if a cow is placed in a cell (i,j), the beauty of the photo is increased by aij (0≤aij≤1000) units.
Determine the maximum possible beauty of the correct placement of cows.
Input
The first line contains the number N. Each of the next N lines contains N integers. The j-th number in the i-th row from the top is the value aij.
Imprint
Print one integer - the maximum possible beauty of the resulting photo.
Examples
| # |
Input |
Output |
Explanations |
| 1 |
4
3 3 1 1
1 1 3 1
3 3 1 1
1 1 3 3
|
22 |
In this example, maximum beauty can be achieved with the following placement:
CC..
..CC
CC..
..CC
The beauty of this placement is 3+3+3+1+3+3+3+3=22. |
| |
![]()
|
|
Темы:
hash
Prefix sums(minimums, ...)
Bust
Huckleberry Finn has two strings s and t of the same length n.
Huckleberry Finn likes strings to have the same prefixes (beginnings), so he can swap two characters in string s to make the common prefix of strings s and t larger.
However, this trick is rather tedious, so Huckleberry Finn will either not do it at all, or will do it exactly once.
Help Huckleberry Finn determine the longest common prefix length of strings s and t that he can get.
Input:
The first line contains a natural number n (1 <= n <= 200000) - the length of strings s and t
The second line contains a string s, consisting of lowercase Latin letters.
The third line contains a string t consisting of lowercase Latin letters.
Output:
Print one natural number - the maximum length of the common prefix s and t, which can be obtained by exchanging two characters in the string s at most once.
Examples:
| Input |
Output |
3
wai
add |
1 |
5
qdyid
xreac |
0 |
| |
![]()
|
|
Темы:
hash
Prefix sums(minimums, ...)
Bust
At the beginning of the 18th century, a group of European explorers arrived on an island inhabited by a group of tribes that had never come into contact with representatives of European civilization.
To successfully establish contacts with the natives, the leader of the group plans to give a gift to the leader of each tribe he meets. To this end, he brought a long chain of glass, similar to precious stones.
Let's represent the string as a string s, consisting of small letters of the English alphabet, where each letter means the type of piece of glass at the corresponding position.
The researchers are going to cut the chain into some fragments, and then hand over exactly one fragment to the leader of each tribe encountered by the group. The research leader decided to split the chain into fragments according to the following rules:
- In order not to spend a lot of time on cutting, each fragment should be a group of adjacent pieces of glass in the chain, that is, a substring of the string s.
- All pieces of glass must be used, that is, each piece of glass must be included in exactly one fragment.
- Because the researchers don't know how the aborigines will value certain types of glass, they want each chief to get the same set of glass without regard to order. In other words, for any type of glass, the number of glass of this type must be the same in each of the fragments.
- Researchers don't know how many tribes live on the island, so the number of prepared fragments should be as large as possible.
Help the manager determine the maximum number of fragments that can be obtained.
Input:
The first line contains the string s (1 <= |s| <= 5000000).
Output:
Print a single number - the maximum possible number of fragments into which the researchers can cut the chain they have without violating any of the conditions formulated by the group leader.
Examples:
| Input |
Output |
| abbabbbab |
3 |
| aabb |
1 |
Explanations:
In the first example, researchers can break the chain 'abbabbbab' fragments 'abb', 'abb', 'bab', then the leader of each tribe they meet will get one glass of type 'a' and two pieces of 'b'.
In the second example, the string cannot be divided into more than one fragment of the chain, observing all the conditions.
| |
![]()
|
|
Темы:
meet in the middle
Bust
A rectangular field of size n*m is specified. Each cell contains a non-negative integer. You need to count the number of paths from cell (1,1) to cell (n,m) that satisfy the following conditions.
1) From each cell, you can only move down or right without leaving the field.
2) The bitwise exclusive OR of all numbers on the path must be equal to k.
Find the number of matching paths for the given field.
Input
The first line contains three integers n, m and k (1 <= n, m <= 20, 0 <= k <= 1018) - the height and width of the field, and the number k.
The following n lines each contain m integers ai,j, where j -th element of i-th row is equal to ai,j (0 <= ai,j < ;= 1018).
Imprint
Print one integer - the number of paths that satisfy all conditions.
Examples
| # |
Input |
Output |
| 1 |
3 3 11
2 1 5
7 10 0
12 6 4
| 3 |
| 2 |
3 4 2
1 3 3 3
0 3 3 2
3 0 1 1
| 5 |
| |
![]()
|
|
Темы:
Depth walk
Bust
Bor
Blaze sends movement orders to his troops, gathered from the inhabitants of one of the shadows. Unfortunately, they don't understand Amber, so Blaze has to send them messages in their own language.
Therein lies the problem: the Amberian prince does not know the spelling of this language well, so he sometimes makes mistakes in words, but no more than one mistake in a word.
There are a lot of words in the language, so if at least one letter in a word changes, then its meaning can change dramatically. If the army does not correctly understand the order, then the entire military campaign may fail. Therefore, it is very important for Blaise to check the correct spelling of words. He decided to ask you to help him.
You must create a program that will output in lexicographic order all the possible words that Blaise could have tried to write, given that he could have made a mistake 1 time.
Input
The first line contains numbers n and m - the number of orders given by Blaze and the number of commands understood by his troops, respectively. (1 <= n, m <= 5000)
The next line takes m words as input - commands that Blaze's troops understand.
In the next n lines, words are given as input - orders given by Blaze.
All strings are less than 100.
Output
Print n lines: line number i contains the answer to the problem for Blaze's order number i. Lines that are the answer to this query are displayed on a single line separated by a space.
Example
Input
5 5
is in if on of
it
in
of
ij
op
Output
if in is
if in is on
if of on
if in is
of on
(c) Evgeny Grigoriev
| |
![]()
|
|
Темы:
One-Dimensional Arrays
Bust
Known points (3, 1 or 0) received by a football team for a number of games in the order they were played. It is known that the team won at least one game and lost at least one game.
What happened before: the first win (3 points) or the first loss (0 points)?
The first line contains the number of games played by the team (not less than 2 and not more than 15).
The second line contains points for each game played.
If the win occurred earlier, then output the word WIN.
If the loss occurred earlier, then output the word LOSE.
Examples
| # |
Input |
Output |
| 1 |
4
1 0 1 3
|
LOSE
|
| |
![]()
|
|
Темы:
for loop
One-Dimensional Arrays
Bust
N boxes are arranged in a row. Initially, the ith box on the left contains ai candies. Gromozeka chooses a box containing at least one candy, and eats one of the candies in the selected box. He can perform this action any number of times. His goal is to ensure that any two adjacent boxes contain no more than x candies.
Find the minimum number of operations required to achieve Gromozeka's goal.
Input
The first line contains two numbers N (\(2<=N<=10^5\)) and x ;(\(0<=x<=10^9\)). The second line contains N integers ai (\(0<=a_i<= 10^9\)).
Imprint
Output the answer to the problem.
Examples
| # |
Input |
Output |
Explanations |
| 1 |
3 3
2 2 2
| 1 |
You must eat one candy in the second box. Then the number of candies in each box will be (2,1,2). |
| 2 |
6 1
1 6 1 2 0 4
| 11 |
For example, you can eat six candies in the second box, two in the fourth, and three in the sixth. Then the number of candies in each box will be (1,0,1,0,0,1). |
| 3 |
5 9
3 1 4 1 5
| 0 |
Goal already reached |
| 4 |
2 0
5 5 |
10 |
All candies must be eaten. |
| |
![]()
|