Module: (Java) Routinen. Rekursion.


Problem

5/10

Rekursion und Iterationen

Theory Click to read/hide

Um die Ansicht zu verstehen, müssen wir die Ansicht verstehen. ♪
Итерацияin der Programmierung im weitesten Sinne die Organisation der Datenverarbeitung, bei der die Aktionen wiederholt werden, ohne sich selbst (im Gegensatz zu der Herausforderung) zu beeinträchtigenVeranstaltungen) In engem Sinne ein Schritt in der zyklischen Datenverarbeitung.
Häufig verwenden die literarischen Algorithmen der aktuellen Schritte das Ergebnis der gleichen Operation oder Operation, wie zuvor berechnet. Ein Beispiel für solche Berechnungen ist die Berechnung von Wettbewerbsverhältnissen.
Das einfache Beispiel des durch die Verwendung von Maisverhältnissen berechneten Wertes ist: - Ja.
Berechnung des Wertes an jedem Schritt (Berechnung) ist - Ja. Bei der Berechnung des Wertes - Ja., wir nehmen die Sache, die bereits erhalten ist.- Ja.♪

Die Zahl kann auch mit Hilfe beschrieben werden рекуррентной формулы:



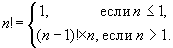
Es sei darauf hingewiesen, dass diese Beschreibung nur eine wiederkehrende Funktion ist.
Das ist die erste Linie.- Ja.() ist der Grundfall (Bedingungszustand) und die zweite Zeile ist der Übergang zum nächsten Schritt.
Die wiederkehrende Fluktuation der Fabrik wird wie folgt aussehenVergleichen Sie den Algorithmus des Ortes zu normalem nicht wiederkehrenden
int Factorial(int n){
wenn
Rückgabe n * Factorial(n-1);
die Rückgabe 1;
♪
x = 1;
für (i = 2; i À= n; i+++)
x = x * i;
Printf("%d,x)

Es ist zu verstehen, dass die Herausforderung der Funktionen zusätzliche Overhead-Kosten mit sich bringt, so dass die nicht-curriculare Berechnung etwas schneller wäre.
Fazit: Wo Sie ein Programm mit einem einfachen heterogenen Algorithmus ohne Vorlesung schreiben können, müssen Sie ohne Vorlesung schreiben. Aber es gibt eine große Klasse von Aufgaben, bei denen der Rechenvorgang nur durch das Feld durchgeführt wird.
Andererseits werden die wiederkehrenden Algorithmen am häufigsten verstanden.

Problem

Bestimmen Sie die Funktion K(n), die die Anzahl der Figuren in der zugeordneten Zahl n zurückgibt:


Schreiben Sie eine sympathische Rolle bei der Berechnung der Anzahl der Zahlen in Art n.

time 1000 ms
memory 32 Mb
Rules for program design and list of errors in automatic problem checking

Teacher commentary

Insert the missing code snippets
Java
Write the program below 
import java.util.Scanner;
public class Main {

static int CountDigit(int n)
{          
return 1+CountDigit(n/10);
}

public static void main(String[] args) {
     Scanner in = new Scanner(System.in);
     int n;
     n = in.nextInt();
     System.out.println(CountDigit(n));
   }      
}

     

Program check result

To check the solution of the problem, you need to register or log in!