Der Zwillingsbaum der Suche ist ein binärer Baum, für den die folgenden zusätzlichen Bedingungen erfüllt sind (der Baum der Suche):
♪ Beide Seiten, links und rechts, sind Zwillingsbäume der Suche.
♪ Die Schlüssel der Daten sind kleiner als der Wert des Datenschlüssels zum X-Hub selbst.
♪ Alle Rechteinhaber haben einen beliebigen X-Knoten, die Schlüssel sind größer oder gleich (manchmal streng mehr, je nach Aufgabe) als der Wert des X-Datenschlüssels selbst.
Problem:
Es scheint, dass seine Struktur ermöglicht verschiedene Operationen (Lieferung, Suche, Entsorgung) für O(logn), aber es ist nicht.
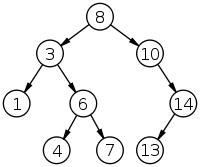
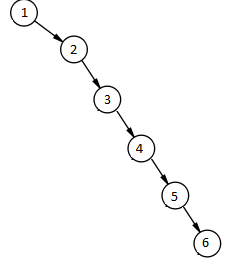
Das Zweirad der Suche kann den Bambus erreichen, dann werden alle Operationen für O(n) durchgeführt. Dies ist ein Beispiel für diesen Baum:
Entscheidung:
1989 lösten Sidel und Aragon das Problem, indem sie dem Deramid (Holz + Pyramide) vorschlugen.
Die Bäume halten ein Paar (X.Y) in Form eines binären Baumes so, dass es der binäre Baum der Suche nach x und binäre Pyramide durch y ist. vorausgesetzt, dass alle X und alle Y unterschiedlich sind, enthält ein bestimmtes Element des Baumes (X)0),Y0)(d) Alle Komponenten in der linken Unterstützung von X RP X0)alle Elemente im Recht X grad X unterstützen0)sowie links und rechts zu unterstützen, haben wir:0)♪
P.S. X und Y können immer noch gleich sein, es ist keine große Sache, obwohl die Wahrscheinlichkeit einer solchen Situation sehr gering ist.
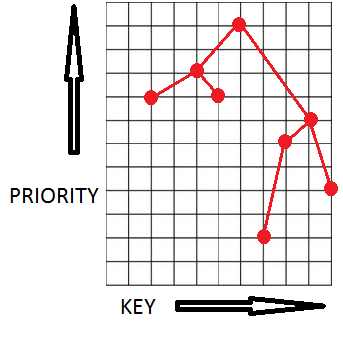
Decartov Baum
Decarto-Baum ist eine auf Deramid basierende Datenstruktur.
DEZARTEN ÜBER NUCLEAR
Um einen Dekartbaum zu speichern, werden wir eine Struktur Node (ein Knoten) erstellen, die ein Dombaum sein wird. Es wird Referenzen (Indikatoren) auf das linke und rechte Kind, Key(x), Priority(y).
Im Code:
HTML generiert mit Hilite. ich
Struct Node {~}
Node♪ link_son;
Node♪ Rechts_son;
Int-Schlüssel, Priorität;
?
Vorrang muss durch Unfall erzeugt werden:
HTML generiert mit Hilite. ich
♫include PEROTING#include Portuguese#include PortugueseVerwendung Namespace std;
In Haupt(lacht)
{~}
srand(time)NULL()
in Priorität = rand();
zurück 0);
♪
:
HTML generiert mit Hilite. ich
Node♪ Jetzt = neue Nein.NULL♪ NULLk, pr};
Unser Baum wird zwei grundlegende Fähigkeiten haben:
(1) Es kann in zwei Wälder geschnitten werden (split)
(2) Zwei Wälder können mit einem (Merge) verbunden werden
Durch diese Operationen erhalten wir korrekte Bäume.
Beschreibung der Operationen:
(1) Split - wird einen Baum um zwei Schlüssel k schneiden. Dadurch wird der erste Baum alle Schlüsselspitzen im [min(key); k) haben. In der zweiten [k; max(key)].
Split ist eine wiederkehrende Funktion, die ein Paar Knoten* zurückgibt. Als Parameter, die Wurzel des Baumes, den wir abschneiden, und der Schlüssel k wir abschneiden.
Aktion:
Sehen wir den Schlüssel zum aktuellen Top. Macht Sinn, dass, wenn sein Schlüssel stat= der Schlüssel, den wir abschneiden, müssen wir den linken Sohn (wiederkehrendes Starten) schneiden. Anstelle des linken Sohnes haben wir zwei Seiten: die linke, wo es eine Spitze mit den rechten Schlüsseln und die rechte, in der alle anderen bleiben. Um schließlich zwei korrekte Bäume zu haben, müssen wir das richtige Gleichgewicht aus dem Schneiden des linken Sohnes mit dem linken Baumkind machen, das wir ursprünglich betrachtet haben. Die Bäume werden zurückgegeben.
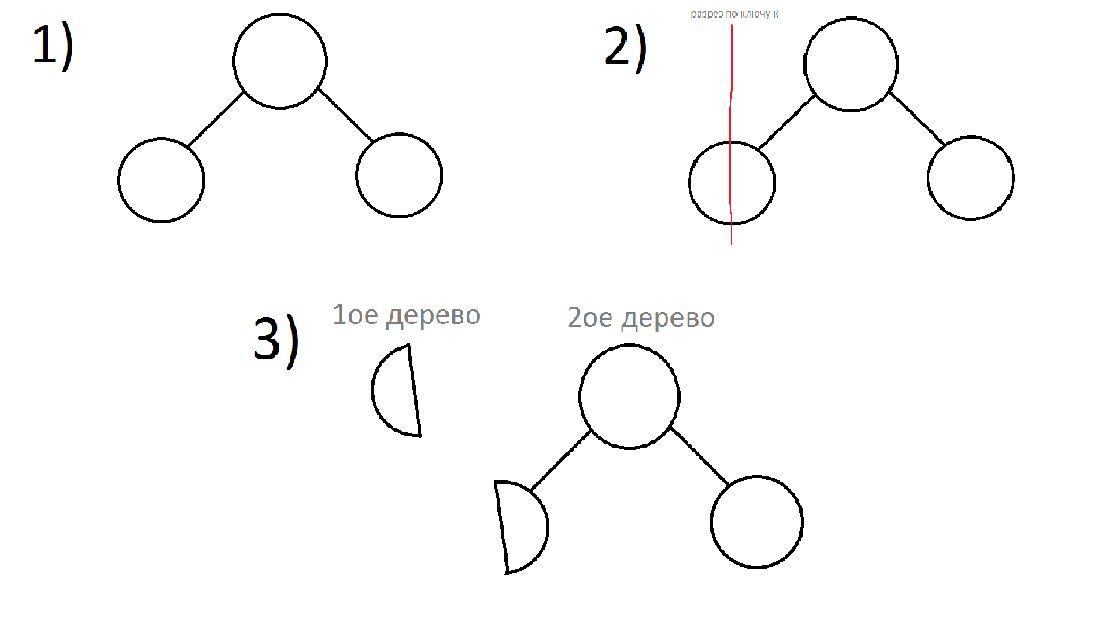
Wenn der Schlüssel zum aktuellen Knoten buyant ist als der Schlüssel, an dem der Schlüssel kleiner ist, schneiden Sie den rechten Halt. Anstelle des rechten Sohnes haben wir zwei Seiten: die rechte Spitze mit den rechten Schlüsseln und die linke, in der alle anderen bleiben. Um schließlich zwei korrekte Bäume zu haben, müssen wir das linke Gleichgewicht der Exzision des rechten Sohnes zum rechten Baumkind machen, das wir ursprünglich betrachtet haben. Die Bäume werden zurückgegeben.
P.S. Genau die gleichen Aktionen wie die Linke, genau das Gegenteil.
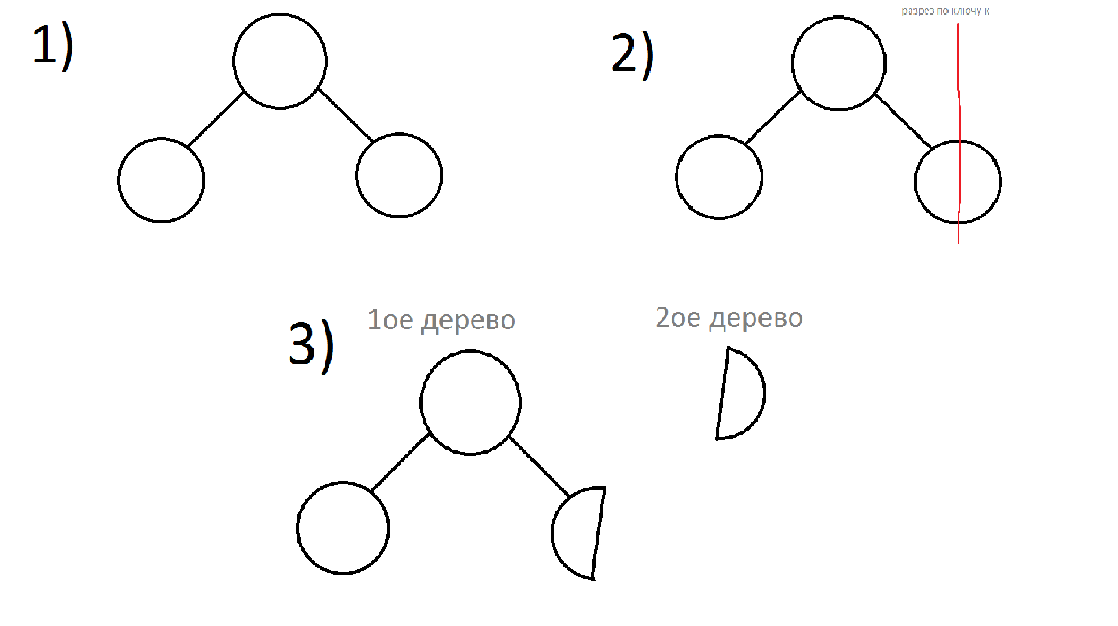
P.S. Wenn die Spitze, die wir nicht haben (die Flyer haben NULL Referenzen), dann müssen zwei Leerstellen zurückgegeben werden.
(2) Verschmelzung - verbinden zwei Bäume in einem, je nach Baumprioritäten.
Merge ist eine wiederkehrende Funktion, die Node* zurückgibt. Die Parameter sind 2 Node*.
Aktion:
Vergleichen Sie die Prioritäten der beiden Baumdaten. Wenn die Priorität der Linken größer ist, werden wir das rechte Kind mit dem rechten Baum verbinden.

Wenn mehr der richtigen Priorität, verbinden wir sein linkes Kind mit dem linken Baum.
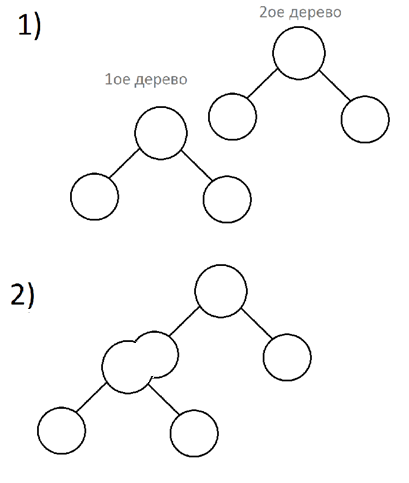
Wichtige Anmerkung:
Wir weisen darauf hin, dass die Wurzel des Baumes und alle Flyer in einem Wüstenbaum keine Kinder haben (d.h. Null-Indikatoren).
Der Bezug auf einen Null-Indikator führt zu einer Fehlleistung, so viele Event-Operatoren können dieses Problem oder einen bestimmten Knoten lösen, der ein vibrierendes Top sein wird. Und statt Null-Indizes machen wir einen Index für Knoten. In einem solchen Fall gibt es keinen Leistungsfehler, aber solche Spitzen müssen sorgfältig verwendet werden.
Node* leer = neue Node {NULL, NULL, 0, 0}; - Fissile Peak (Desert).
Dann wird die Schaffung eines neuen Gipfels wie folgt sein:
Node* jetzt = neu Node {leer, leer, k, pr};
Die Spaltung und Zusammenführung sollte getrennt behandelt werden, wenn der Baum leer ist, nämlich:
(1) Wenn Sie die Leere schneiden, gibt es zwei Leerzeichen.
(2) Wenn Sie etwas mit nichts verbinden, wird es sich nicht ändern.
Holzkonstruktion und -änderung:
Um den Baum zu ändern, benötigen wir zwei Funktionen:
(1) Einsatz
Es wird eine k-Taste k zum Baum hinzufügen.
Um dies zu tun, erstellen wir einen neuen k-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-a-
(2) Erase
Es wird den k Schlüssel k aus dem Baum entfernen.
Zum Start-up, der Split-Baum auf dem Schlüssel k. Wie wir uns erinnern, wird der erste Baum alle Schlüsselspitzen im [min(key); k) und im zweiten [k; max(key)] haben. Weiter oben, das Recht auf den Schnitt des Baumes auf dem Schlüssel k + 1. Letztlich haben wir drei Unterstützung, mit Schlüsseln weniger als k, Schlüssel k und Schlüssel mehr als k. C-merge-them mit Schlüsseln weniger und mehr k, und der Knoten mit dem Schlüssel k ist einfach vergessen.
Baumbau:
Zunächst haben wir den Knoten der Wurzel, der den „Atm“ repräsentieren wird. Dann legen wir einfach alle notwendigen Knoten in den Baum ein.
Wartung des Parameters im Dekarta-Baum
In dieser Struktur möchten Sie wahrscheinlich einen Parameter (eine Summe, ein Minimum usw.) aufbewahren, da alle Anfragen für O(log n) gestellt werden.
Erstellen Sie ein neues Feld in einer Struktur, die für den Wert der benötigten Parameter in der Unterstützung verantwortlich ist. Der Wert des Parameters in einem bestimmten Knoten ist der Wert in der Unterstützung, dass die Wurzel des Knotens ist.
Um den richtigen Parameter aufrechtzuerhalten, werden wir ein Updateverfahren einführen.
Das Update wird den Parameter durch seine Kinder und sich selbst wiedergeben.
Zum Beispiel:
HTML generiert mit Hilite. ich
Vgl.- KategorieSumme = Vgl.- Kategorielinks_son- KategorieSumme + Vgl.- KategorieRechtsanwälte- KategorieSumme + Vgl.- KategorieSchlüssel;
Vgl.- Kategoriemin = min(v)- Kategorielinks_son- Kategoriemin, v- KategorieRechtsanwälte- Kategoriemin), v- KategorieSchlüssel
Vgl.- KategorieGröße = Vgl.- Kategorielinks_son- KategorieGröße + Vgl.- KategorieRechtsanwälte- KategorieGröße + 1
Wo v der aktuelle Knoten ist.
Das Update sollte die fictit Peaks nicht aktualisieren.
Vor jeder Rückkehr zu teilen und zu verschmelzen, werden wir aktualisieren, was wir zurückgeben. Wir bekommen schließlich die richtigen Werte.
Nun, um den Parameter in einem bestimmten Backup zu kennen, Sie-split-- das ist Unterstützung und wir gehen in das Parameterfeld. Es wird definitiv eine Anpassung geben.
DEZEMBER DER NICHT-NAL
Der Dekartobaum ist ein leicht modifizierter Dekartobaum mit einem klaren Schlüssel. Jeder Peak wird nun nicht durch einen Schlüssel, sondern durch eine Seriennummer gekennzeichnet. So wird der Baum nun die folgenden Eigenschaften haben: Für jede Oberseite wird beobachtet, dass alle Spitzenzahlen in der linken Rückseite kleiner sind und das Recht auf Unterstützung größer ist als seine eigene Zahl. So kann man einfach die geordnete Struktur des Baumes vergessen, und es wird tatsächlich von einem Zwillingsbaum der Suche zu einer gewöhnlichen Masse transformiert.
Durchführung:
Es ist unvorstellbar, die Seriennummern in klarer Form zu halten, und ihre Änderung wird eine lange Zeit dauern, so dass wir die folgende Tatsache verwenden: die Seriennummer jedes Peaks ist gleich der Lampe mit einer geringeren Anzahl, d.h. die Größe der linken Unterstützung. Die Größe der Unterstützung ist bereits vorhanden.
Aber jetzt ändert sich die Spaltung, weil der Schlüssel weg ist.
Genau: Jetzt kann der Baum nur nach Größe geschnitten werden. Der Handlungsalgorithmus bleibt gleich (siehe oben), nur die Bedingung, unter der wir definieren, welche der beiden Kinder wir in isothisch eingehen werden.
Lassen Sie uns nun einen Baum v in der Größe k (entsprechend zwei Bäume von k und v-konsize - k) abschneiden. Jetzt gibt es zwei offensichtliche Fälle:
(1) Die Größe des linken Trägers ist größer oder gleich k. Dann müssen wir das linke Kind schneiden.

(2)
Die linke Stütze ist kleiner als k. Das rechte Kind muss geschnitten werden, aber in diesem Fall alle linke Unterstützung und die Oberseite wird die Prästigation eines k-förmigen Baumes, der in den aktuellen Schritt zurückkehrt, so dass das rechte Kind nach Größe k-v-ferleft_son-Statesize-1 geschnitten werden muss.
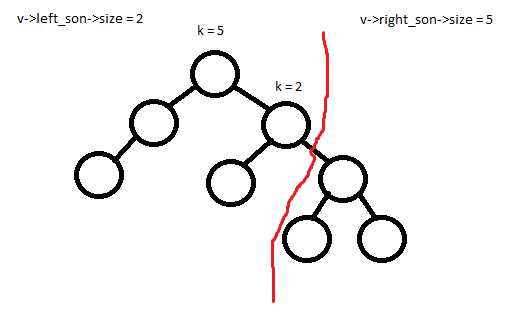
Operation Zusammenführung ändert sich nicht.
Es gibt auch eine leichte Änderung (und es ist einfacher) einen dekarten Baum zu bauen. Die Insertions- und Löschfunktionen sind nicht mehr notwendig, da beim Hinzufügen der Peaks am Ende des Baumes (d.h. die Zahl ist die größte) eine neue hinzugefügt werden muss. In der Tat, in jedem Schritt würde es aussehen wie
wurzel = fusion(root, p)
wo p der neue Gipfel ist (siehe oben für die Ankündigung).
Anwendungen:
Jetzt haben wir eine starke Datenstruktur, die massive Operationen wie die Entfernung und Lieferung von Sublets über die Zeit O (log(n)) bewältigen kann.
Beispielsweise sollte der Schnitt [l;r] bis zum Ende der Masse bewegt werden. Zu diesem Zweck werden wir unseren Baum auf drei Stufen schneiden:
(1) Wir schneiden es ab.
(2) Rechtsteil vom Schneiden bis r - l + 1
L, M, R (links, Mitte, rechts) Abmessungen l - 1, r - l + 1 und n - r jeweils erhalten. Der M-Baum wird derjenige sein, den wir brauchen.
Wir werden sie einfach wieder verbinden, aber in einer anderen Reihenfolge:
Wurzel = Merge(L, R), M);
Massenbetrieb:
Massenoperationen können über einen Deckart-Baum auf einem nicht-gebietsbezogenen Schlüssel (Abstand, Cut-off, etc.) durchgeführt werden. Die gleiche Bedeutung wie andere Datenstrukturen: Erstellen Sie ein neues Feld innerhalb von Node, um für die faule Änderung des Knotens verantwortlich zu sein. Wir werden auch eine Push-Methode erstellen, die die notwendige Neuberechnung des Knotens vornehmen und Informationen an Kinder übermitteln wird. Das Push-Verfahren muss zu Beginn der Operation Split ausgelöst und zusammengeführt werden.
Beispiel für die Schubmethode, die eine Massenzugabe ist. Es gibt eine Unterstützung und einen Wert im Baum.
HTML generiert mit Hilite. ich
Leer Druck(Node)♪ (v)
{~}
wenn (v) == sync, berichtigt von elderman == leer)
zurück; / nicht verarbeitete FiktitspitzenVgl.- KategorieSumme = (v)- KategorieLazy ♪ Vgl.- KategorieGröße,
Vgl.- KategorieWert = Vgl.- KategorieLazy;
Vgl.- Kategorielinks_son- KategorieLazy = Vgl.- KategorieLazy; / Ins linke Kind fallenVgl.- KategorieRechtsanwälte- KategorieLazy = Vgl.- KategorieLazy; / In das richtige Kind fallenVgl.- KategorieLazy = 0); ♪ Füge nichts hinzu♪
Um nun einen Massenbetrieb auf dem Schnitt durchzuführen, splitst du genug, um die notwendigen Cut-offs zu haben und das für die faulen Operationen am Knoten verantwortliche Feld zu ändern, das die Wurzel dieses Sublet sein wird. Dann steck den Baum in ein Stück zurück.
Es ist auch erforderlich, die notwendigen Schnitte zu schneiden und die Bedeutung des Feldes zu fragen, um den Wert der Unterbasis zu kennen.
Es ist garantiert, dass es richtig funktioniert, wenn richtig implementiert.
Knochen.
Der Dekartobaum kann auch einen Schnitt auf den Schnitt machen! Wie ist das möglich? Erinnern Sie sich an die Natur des Dekartobaums in einem nicht-wohnlichen Schlüssel - für jede Spitze sind alle Spitzenzahlen auf der linken Seite kleiner und das Recht auf Unterstützung ist größer als ihre eigene Nummer. Zu diesem Zeitpunkt muss die Ausklinkung genau das Gegenteil sein, so ist es nur genug, dass jeder Knoten die Plätze seines linken und rechten Kindes ändert (swap(v-stateleft_son, v-tarright_son). Wieder einmal werden wir ein Feld der faulen (lene change) einrichten, das von der Veränderung der Plätze der Kinder spricht. Indem wir die wahre Bedeutung der Flanke drängen, ändern wir die Plätze der Kinder und machen es gleich falsch. Es muss jedoch darauf geachtet werden, Informationen an Kinder zu übermitteln! Es ist nur zu sagen, dass die Faulen die Wahrheit sein muss, weil es die Wahrheit zuvor gewesen sein könnte, was bedeutet, dass wir an diesem Punkt auf das, was eingesetzt wird, umdrehen müssen und daher einfach keine Veränderung hinterlassen (durch Sie erhalten die ursprüngliche Masse zweimal). Die Bedeutung von Faul sollte jedes Mal geändert werden.
HTML generiert mit Hilite. ich
Leer Druck(Node)♪ (v)
{~}
wenn (v) == sync, berichtigt von elderman == leer Vgl.- KategorieLazy == sync, berichtigt von elderman == falsch) / Wenn du dich nicht umdrehen musst, gehen wir sofort raus.zurück;
Swaps- Kategorielinks_son, Vgl.- Kategorierechts_son);
Vgl.- Kategorielinks_son- KategorieLazy ^= wahr;
Vgl.- KategorieRechtsanwälte- KategorieLazy ^= wahr;
Vgl.- KategorieLazy = falsch;
♪
(c) Kurbatov E., 2018