Para comprender la recursividad, debe comprender la recursividad...
Iteración en programación — en un sentido amplio: organización del procesamiento de datos, en la que las acciones se repiten muchas veces, sin dar lugar a llamadas a sí mismas (a diferencia de %BA%D1%83%D1%80%D1%81%D0%B8%D1%8F" title="Recursion" >Recursiones). En el sentido estricto, mdash; proceso de procesamiento de datos cíclico de un paso.
A menudo, los algoritmos iterativos en el paso actual (iteración) utilizan el resultado de la misma operación o acción calculada en los pasos anteriores. Un ejemplo de tales cálculos es el cálculo de las relaciones de recurrencia.
Un ejemplo simple de un valor recursivo es el factorial:
\(N!=1 \cdot 2 \cdot 3 \cdot \ ... \ \cdot N\)
El cálculo del valor en cada paso (iteración) es
\(N=N \cdot i\) . Al calcular el valor de
\(N\), tomamos el valor ya almacenado
\(N\).< br />
El factorial de un número también se puede describir usando la
fórmula recurrente:
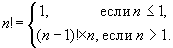
Puede notar que esta descripción no es más que una función recursiva.
Aquí la primera línea (
\(n <= 1\)) — este es el caso base (condición final de la recursividad) y la segunda línea es la transición al siguiente paso.
| La función factorial recursiva se vería así |
Compare el algoritmo para encontrar el factorial de la forma habitual no recursiva |
|
factorial int(int n){
si (n > 1)
devuelve n * Factorial(n - 1);
de lo contrario devuelve 1;
}
|
x = 1;
para (i = 2; i <= n; i++)
x = x * yo;
printf("%d",x);
|
Debe entenderse que las llamadas a funciones implican una sobrecarga adicional, por lo que un cálculo factorial no recursivo será un poco más rápido.
Conclusión: donde puede escribir un programa con un algoritmo iterativo simple, sin recursión, entonces necesita escribir sin recursión. Pero aun así, existe una gran clase de problemas en los que el proceso computacional se implementa solo mediante recursividad.
Por otro lado, los algoritmos recursivos suelen ser más comprensibles.