Las combinaciones de n elementos por k son compuestos que se pueden formar a partir de n elementos, reuniendo k elementos en cada conexión; mientras que las conexiones se diferencian entre sí solo por los elementos mismos (no se tiene en cuenta la diferencia en el orden de su disposición).
Por ejemplo, las siguientes combinaciones se pueden formar a partir de 3 elementos (a,b,c)(a,b,c) 2 cada uno: ab,ac,bc.
El número de todas las combinaciones posibles que se pueden formar a partir de n elementos por k se indica mediante el símbolo

y calculado por la fórmula:
Hay dos formas de encontrar el número de combinaciones

1. Encuentre n!, k!, (n – k)! y según la fórmula anterior, calculamos la cantidad, pero a partir de – debido a un posible desbordamiento, este método se puede utilizar con n <= 12.
2. Con programación dinámica.
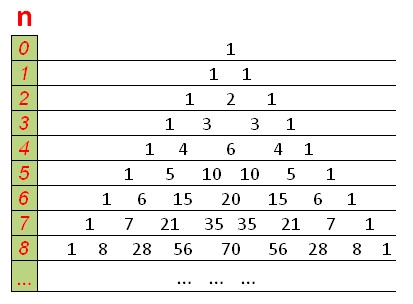
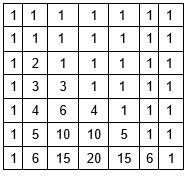
El DP se verá como el triángulo de Pascal, con unos en la parte superior y en los bordes, y cada número es igual a la suma de los dos números que están arriba.
Una función que cuenta el número de combinaciones usando programación dinámica en O(n ^2 ):
int C(int n, int k)
{
vector<vector<int> > dp(n + 1, vector<int>(n + 1, 1)); // Crear una matriz de dp de tamaño (n + 1, n + 1)
para (int i = 0; i <= n; i++) // Complete la i-ésima línea de la matriz
{
para (int j = 1; j < i; j++)
{
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; //recalcular (i;j) la posición a través de (i - 1; j - 1) y (i - 1; j)
}
}
return dp[n][k]; //valor devuelto
}