Problem
Una araña y una araña flotan en el lago sobre dos ramas. No pueden nadar, por lo que solo pueden encontrarse cuando las ramas se tocan.
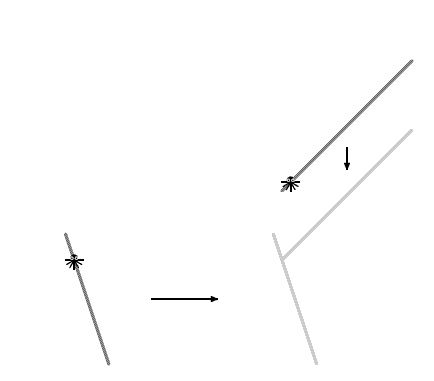
Suponiendo que las ramas están en forma de segmentos, y que nadan a velocidades constantes, determinan cuánto tardan en encontrarse con el desafortunado artrópodo.
Entrada
El archivo de entrada contiene 12 números: x1, y1, x2, y2, x 3, y3, x4, y4, v1x, v 1y, v2x, v2y. Las coordenadas de los vértices del primer segmento: (x1, y1) y (x2, y2), coordenadas vértices del segundo segmento: (x3, y3) y (x4, y4< /sub>), la velocidad del primer segmento (v1x, v1y), la velocidad del segundo segmento (v2x, v2y). Todos los números son enteros y no superan en valor absoluto 104. En el momento inicial de tiempo, las ramas no se tocan. Se garantiza que las ramas tendrán una longitud distinta de cero.
Salida
Ingrese en el archivo de salida el tiempo hasta el momento más cercano en que las ramas se tocan, con un error de no más de 10
−4. Si las ramas nunca se tocan, imprime el número -1.
| Entrada |
Salida |
|
0 0 -1 3
4 4 7 7
3 0
0 -1
|
1.6 |
|
0 0 -1 3
4 4 7 7
10
0 -3
|
-1 |
Olimpiadas por Equipos, Campeonatos de Programación por Equipos de Escolares de San Petersburgo, 2006, Problema E