Problem
Asya ama mucho a los animales. Recientemente compró n gatitos, les dio identificadores numéricos del 1 al n y los colocó en un recinto. La pajarera es una fila de n celdas, también numeradas del 1 al n. Las celdas vecinas están separadas por mamparas de malla, en total hay n & menos 1 mamparas en el recinto. Inicialmente, exactamente un gatito con algún número se instaló en cada celda.
Al observar a los gatitos, Asya notó que son muy amigables y que algunos pares de gatitos que viven en celdas vecinas realmente quieren jugar entre ellos. Para no privarlos de este placer, Asya comenzó a eliminar los tabiques entre las celdas adyacentes, haciéndolas más grandes.
El i-ésimo día, Asya hizo lo siguiente.
Noté que algunos gatitos x
i y y
i, que vivían en celdas vecinas el i-ésimo día, quieren jugar.
Quité la partición entre estas celdas, convirtiéndolas en una sola, en la que terminaron todos los gatitos de las dos celdas anteriores.
Como Asya no devolvió los tabiques, al cabo de n−1 día el recinto se convirtió en una única celda en la que vivían todos los gatitos. Siendo muy pedante, Asya anotó las identificaciones de los gatitos x
i y
i para cada uno de los n−1 días en un diario especial.
Tienes una revista con esta información, pero no sabes cómo se instalaron los gatitos en las celdas en primer lugar. Encuentre cualquier distribución de gatitos en n celdas originales que no contradiga los datos del registro.
Entrada
La primera línea contiene un número entero n (
\(2 \leq n \leq 150000\)) — número de gatitos.
Las siguientes n+1 líneas contienen pares de enteros x
i , y
i (
\(1 \leq x_i , y_i, \leq n,x_i \neq y_i\) ) — identificadores de gatitos, entre las celdas de las cuales se eliminó la partición el día i. Se garantiza que los gatitos xi y yi no están en la misma celda como resultado de la fusión de celdas anterior.
Impresión
Imprime n enteros distintos p
i (
\(1 \leq p_i \leq n\)), donde p
i — el identificador del gatito que habitaba originalmente en la celda número i. Si hay varias respuestas posibles, imprima cualquiera de ellas.
Nota
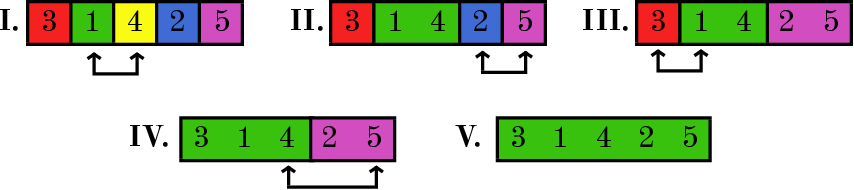
En la respuesta, por ejemplo, se da uno de los posibles asentamientos iniciales de gatitos, hay otras respuestas. La imagen a continuación muestra cómo se fusionaron las celdas para esta colocación inicial de gatitos. Tenga en cuenta que con este arreglo, los gatitos que se hicieron amigos cada día según el diario de Asya están en celdas adyacentes.
| Entrada |
Salida |
5
14
25
3 1
4 5 |
3 1 4 2 5 |