En lugar de solo calcular el hash de una secuencia, podemos almacenar el valor en cada uno de sus prefijos. Tenga en cuenta que estos serán valores hash para secuencias iguales al prefijo correspondiente.
Con tal estructura, puede calcular rápidamente el valor hash para cualquier subsegmento de esta secuencia (similar a las sumas de prefijos).
Si queremos calcular el hash del subsegmento [l;r], debemos tomar el hash del prefijo r y restar el hash del prefijo l-1 multiplicado por p elevado a r-l+1. Por qué esto es así queda claro si escribe los valores en los prefijos y ve qué sucede. Espero que tengas éxito mirando esta imagen.
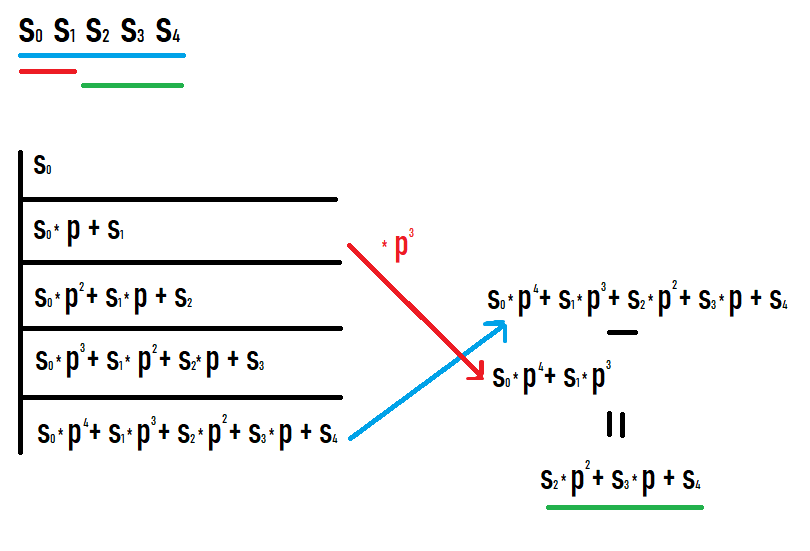
Como resultado de tales acciones, obtenemos un hash de un subsegmento de la secuencia original. Además, este hash es igual al que se consideraría como un hash de una secuencia igual a este subsegmento (no se requieren conversiones adicionales de grados o similares para comparar con otros valores).
Hay dos puntos a aclarar aquí:
1) Para multiplicar rápidamente por p a la potencia r-l+1, es necesario precalcular todas las potencias posibles de p módulo mod.
2) Debe recordarse que realizamos todos los cálculos módulo módulo y, por lo tanto, puede resultar que después de restar los hash del prefijo, obtengamos un número negativo. Para evitar esto, siempre puedes agregar mod antes de restar. Además, no olvide tomar el valor del módulo después de las multiplicaciones y todas las sumas.
En el código se ve así:
#incluye <bits/stdc++.h>
utilizando el espacio de nombres estándar;
typedef long longll;
const int MAXN = 1000003;
// módulo base y hash
ll p, mod;
// prefijo hash y exponentes p
h[MAXN], pows[MAXN];
// calculando el hash del subsegmento [l;r]
ll get_segment_hash(int l, int r) {
return (h[r] + mod - h[l - 1] * pows[r - l + 1] % mod) % mod;
}
int principal()
{
// de alguna manera obtener p y mod
// precalcular potencias p
fuerzas[0] = 1;
para (int i = 0; i < MAXN; i++)
pows[i] = (pows[i - 1] * p) % mod;
//
// solución del problema principal
//
devolver 0;
}