DFS DFS
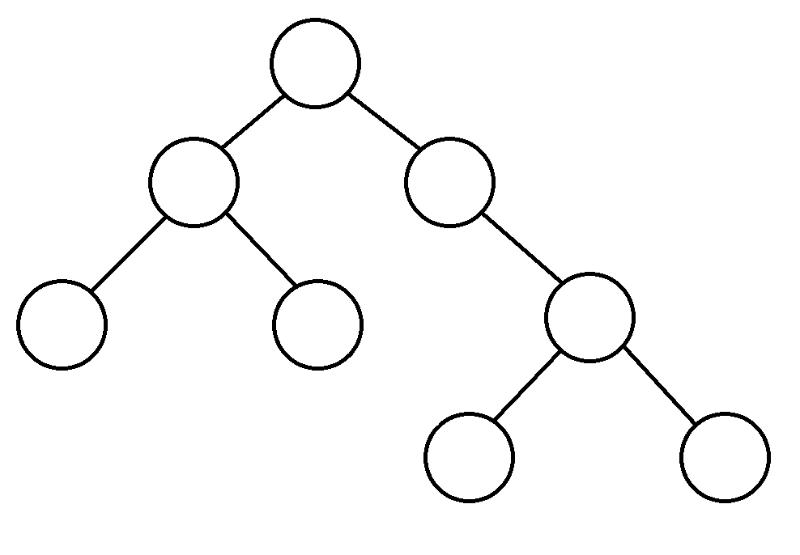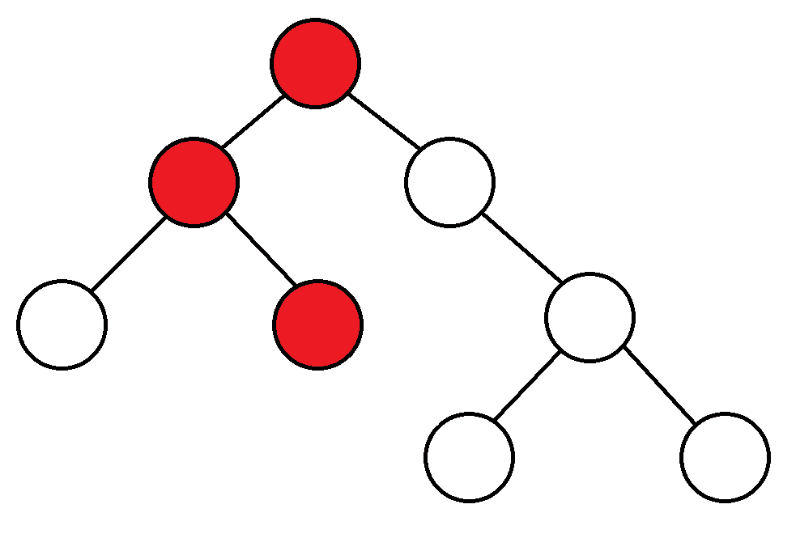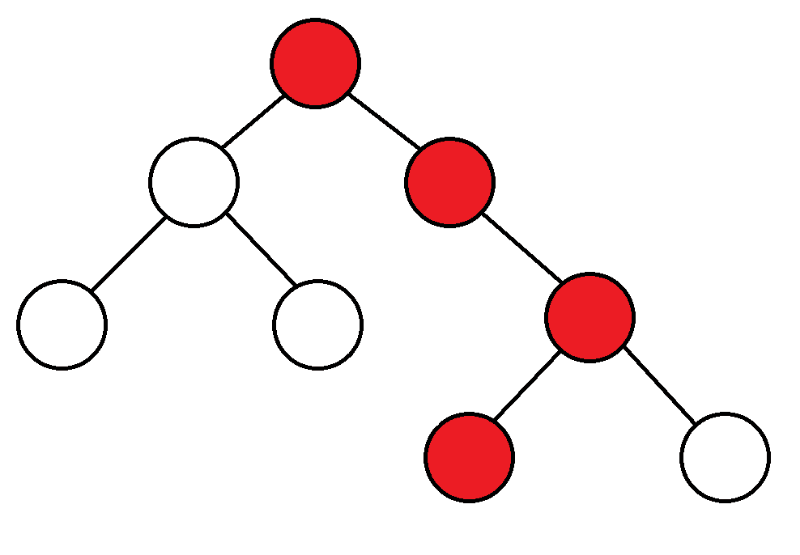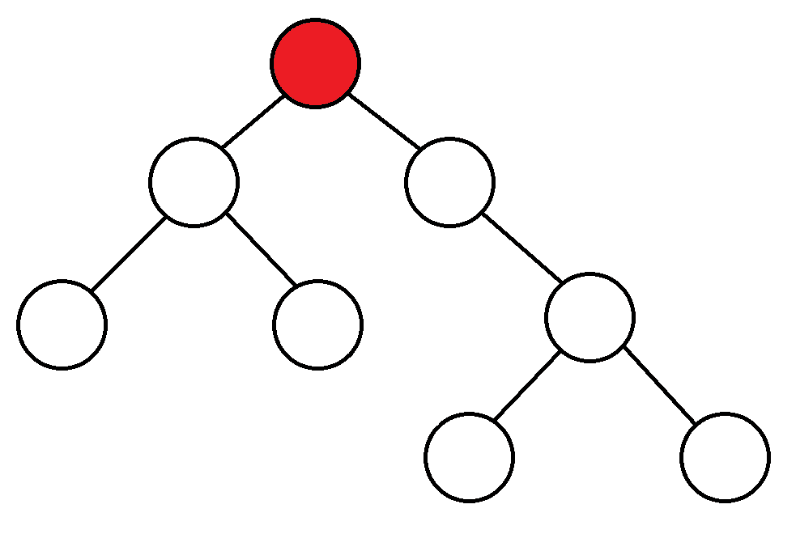
La búsqueda en profundidad ( DFS) es uno de los principales algoritmos de los gráficos. El algoritmo se ejecuta en O(N + M).
Algoritmo
Para empezar, comenzamos desde la parte superior, consideramos los elementos secundarios de esta parte superior y, si nunca los hemos ingresado, comenzamos DFS desde ellos.
|
DFS DFS
La búsqueda en profundidad ( DFS) es uno de los principales algoritmos de los gráficos. El algoritmo se ejecuta en O(N + M).
Algoritmo
Para empezar, comenzamos desde la parte superior, consideramos los elementos secundarios de esta parte superior y, si nunca los hemos ingresado, comenzamos DFS desde ellos.

|
Gráfico bipartito
Gráfico bipartito: un gráfico cuyos vértices se pueden dividir en dos conjuntos para que cada borde conecte el vértices de diferentes conjuntos.
A menudo, en el contexto de gráficos bipartitos, se utiliza el concepto de colores vértices. Dividir un gráfico en dos partes se llama colorear sus vértices con dos colores diferentes. Cada borde debe conectar vértices de un color diferente.
DFS.
Algoritmo
Comenzamos a pintar desde un vértice arbitrario, que pintamos en un color arbitrario.
Al pasar a lo largo de cada borde, pinte el siguiente vértice en el color opuesto.
Si, al iterar sobre los vértices vecinos, encontramos un vértice que ya está pintado del mismo color que el actual, entonces hay un ciclo impar en el gráfico, lo que significa que no es bipartito.
|
El algoritmo se puede describir de la siguiente manera:
Dado un grafo dirigido con n vértices y m aristas. Se requiere renumerar sus vértices de tal manera que cada arista conduzca desde un vértice con un número más bajo a un vértice con uno más alto.
Es decir, se requiere encontrar una permutación de vértices (orden topológico) correspondiente al orden dado por todas las aristas del grafo.
Usaremos la búsqueda en profundidad (dfs(v))
Si agregamos nuestro vértice al comienzo de una lista al momento de salir de \(dfs(v)\) , entonces al final en esta lista obtienes una ordenación topológica.
Por lo tanto, la ordenación topológica deseada — esto se ordena en orden descendente de tiempos de salida.
|