Insertar clasificación
Ordenar por inserción (Ordenar por inserción) — ;algoritmo de clasificación en el que los elementos de la secuencia de entrada se buscan uno a la vez, y cada nuevo elemento entrante se coloca en el lugar adecuado entre los elementos previamente ordenados.
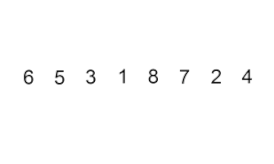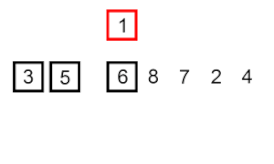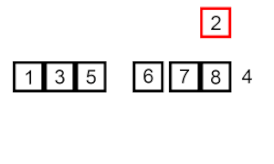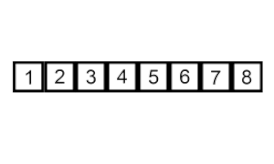
Insertar ordenar – es un algoritmo muy simple pero ineficiente que, sin embargo, tiene varias ventajas específicas que lo hacen relevante incluso después de que se hayan desarrollado muchos otros algoritmos generalmente más eficientes.
Con la ordenación por inserción, no es necesario tener todo el arreglo al frente antes de ordenar. El algoritmo puede recibir un elemento a la vez durante la clasificación. Esto es muy útil si necesitamos agregar más elementos durante la clasificación. El algoritmo insertará el nuevo elemento en el lugar correcto sin "volver a ejecutar" ordenando toda la matriz.
La ordenación por inserción se puede utilizar en la práctica debido a su eficiencia en conjuntos de datos pequeños (~10 elementos).
El problema es este: hay una parte de la matriz que ya está ordenada y desea insertar los elementos restantes de la matriz en la parte ordenada, manteniendo el orden. Para hacer esto, en cada paso del algoritmo, seleccionamos uno de los elementos de datos de entrada y lo insertamos en la posición deseada en la parte ya ordenada de la matriz, hasta que se ordena todo el conjunto de datos de entrada. El método para seleccionar el siguiente elemento de la matriz de entrada es arbitrario, pero normalmente (y para obtener un algoritmo de ordenación estable), los elementos se insertan en el orden en que aparecen en la matriz de entrada.
Implementación algorítmica de este algoritmo
// El elemento nulo se considera una secuencia ya ordenada.
// Por lo tanto, el ciclo comienza desde 1
BUCLE PARA I=1 A N-1 PASO 1
X=A[I]
j=yo
CUANDO J>0 AND A[J-1]>X //buscando un lugar para insertar
INTERCAMBIO A[J],A[J-1]
J=J-1
FIN ADIÓS
A[J]=X
SIGUIENTE YO
Complejidad computacional: \(\displaystyle O(n^{2})\).