Recursión
Un procedimiento o función puede contener una llamada a otro procedimiento dentro de él. Incluso, la subrutina puede llamarse a sí misma. En este caso, a la computadora no le importa. También, como siempre, ejecuta consistentemente los comandos que conoce de arriba a abajo.
Si recuerdas las matemáticas, ahí podrás conocer el principio de inducción matemática. Es el siguiente:
algún enunciado es verdadero para todo n natural si
1. es válido para n = 1 y
2. de la validez del enunciado para cualquier n = k natural arbitrario se sigue que es verdadero para n = k + 1.
En programación, esta técnica se llama recursión.
Recursividad es una forma de definir un conjunto de objetos en términos del propio conjunto, en función de casos base simples.
Recursivoes un procedimiento (función) que se llama a sí mismo directamente o a través de otros procedimientos y funciones.
Ejemplo
def Rec(a):
si (a>0): Rec(a-1)
imprimir (a)
Esquemáticamente, el trabajo de la recursividad se puede representar mediante un diagrama de flujo
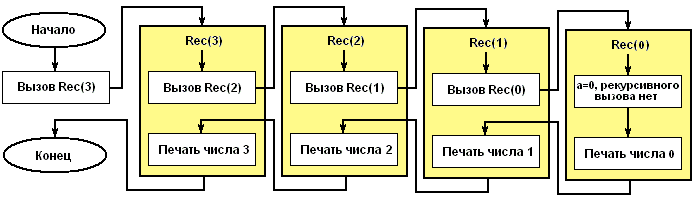
El procedimiento Rec() se ejecuta con el parámetro 3. Luego, dentro del procedimiento con el parámetro 3, se llama al procedimiento con el parámetro 2, y así sucesivamente, hasta que se llama al procedimiento con el parámetro 0. Cuando se llama al procedimiento con el parámetro 0, la llamada recursiva ya no ocurrirá y el procedimiento con parámetro 0 imprimirá el número 0 y saldrá. Luego, el control se transfiere nuevamente al procedimiento con el parámetro 1, también termina su trabajo imprimiendo el número 1, y así sucesivamente. antes del procedimiento con el parámetro 3.
Todos los procedimientos llamados se almacenan en la memoria hasta que completan su trabajo. El número de procedimientos concurrentes se denomina profundidad de recurrencia.
|
Recursividad como reemplazo de bucle
Hemos visto que la recursividad es la ejecución repetida de instrucciones contenidas en una subrutina. Y esto, a su vez, es similar al trabajo del ciclo. Hay lenguajes de programación en los que la construcción de bucle está completamente ausente. Por ejemplo, Prólogo.
Intentemos simular el trabajo del bucle for.
El bucle for contiene una variable de contador de pasos. En una subrutina recursiva, dicha variable se puede pasar como parámetro.
# Procedimiento LoopImitation() con dos parámetros
# Primer parámetro – contador de pasos, segundo parámetro – número total de pasos
def LoopImitation(i, n):
print("Hola N", i) # Declaración que se repetirá para cualquier valor de i
si < n: # Hasta que el contador del bucle sea igual al valor n,
LoopImitation(i + 1, n) # llamar a una nueva instancia del procedimiento,
# con parámetro i+1 (ir al siguiente valor i)
|
Recursión e iteración
Para comprender la recursividad, debe comprender la recursividad...
Iteración en programación - un pasode un proceso cíclico de procesamiento de datos.
A menudo, los algoritmos iterativos en el paso actual (iteración) utilizan el resultado de la misma operación o acción calculada en los pasos anteriores. Un ejemplo de tales cálculos es el cálculo de las relaciones de recurrencia.
Un ejemplo simple de un valor recursivo es el factorial: \(N!=1 \cdot 2 \cdot 3 \cdot \ ... \ \cdot N\).
El cálculo del valor en cada paso (iteración) es \(N=N \cdot i\) . Al calcular el valor de \(N\), tomamos el valor ya almacenado \(N\).< br />
El factorial de un número también se puede describir usando la fórmula recurrente:
\(\begin{ecuación*} n!= \begin{casos} 1 &\text{n <= 1,}\\ (n-1)! \cdot n &\text{n > 1.} \end{casos} \end{ecuación*}\)
Puede notar que esta descripción no es más que una función recursiva.
Aquí, la primera línea ( \(n <= 1\)) es el caso base (condición de terminación de recursividad) y la segunda línea es la transición al siguiente paso.
| Función factorial recursiva |
Algoritmo iterativo |
|
Factorial def(n):
si n > 1:
devuelve n * Factorial(n - 1)
demás:
devolver 1
|
x=1
para i en el rango (1, n + 1):
x = x * yo;
|
Debe entenderse que las llamadas a funciones implican una sobrecarga adicional, por lo que un cálculo factorial no recursivo será un poco más rápido.
Conclusión: donde puede escribir un programa con un algoritmo iterativo simple, sin recursión, entonces necesita escribir sin recursión. Pero aun así, existe una gran clase de problemas en los que el proceso computacional se implementa solo mediante recursividad.
Por otro lado, los algoritmos recursivos suelen ser más comprensibles.
Tarea
En el alfabeto de la lengua de la tribu «Tumba-Yumba» cuatro letras: "K", "L", "M" y "N". Es necesario mostrar en la pantalla todas las palabras que constan de n letras que se pueden construir a partir de las letras de este alfabeto
El problema es un problema normal de fuerza bruta que se puede reducir a un problema más pequeño.
Sustituiremos secuencialmente las letras por la palabra.
La primera posición de una palabra puede ser una de las 4 letras del alfabeto ( K, L, M, N).
Primero, coloque la letra ' K' primero. Luego, para obtener todas las variantes con la primera letra ' K', debe enumerar todas las combinaciones posibles de letras en el resto de n-1 posiciones y .etc. (ver foto)
Por lo tanto, se nos ocurrió una solución recursiva: en un ciclo, pasar por todas las primeras letras posibles (poniendo cada letra del alfabeto en primer lugar) y para cada caso construir todas las "colas" posibles; longitud n-1.
Iteración recursiva de caracteres
Debe detener la recursividad y generar la palabra terminada cuando la parte restante esté vacía (n = 0), es decir todas las letras ya están seleccionadas.
El procedimiento recursivo se vería así:
def TumbaPalabras(palabra, alfabeto, n):
si n < 1:
imprimir (palabra)
devolver
para c en alfabeto:
TumbaPalabras(palabra+c, alfabeto, n - 1)
|
|