hash

Error

En lugar de solo calcular el hash de una secuencia, podemos almacenar el valor en cada uno de sus prefijos. Tenga en cuenta que estos serán valores hash para secuencias iguales al prefijo correspondiente.

Con tal estructura, puede calcular rápidamente el valor hash para cualquier subsegmento de esta secuencia (similar a las sumas de prefijos).

Si queremos calcular el hash del subsegmento [l;r], debemos tomar el hash del prefijo r y restar el hash del prefijo l-1 multiplicado por p elevado a r-l+1. Por qué esto es así queda claro si escribe los valores en los prefijos y ve qué sucede. Espero que tengas éxito mirando esta imagen.



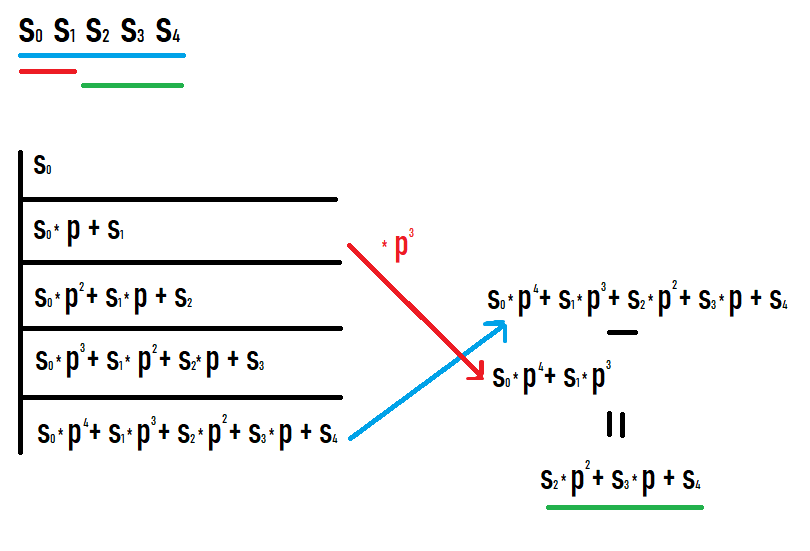
Como resultado de tales acciones, obtenemos un hash de un subsegmento de la secuencia original. Además, este hash es igual al que se consideraría como un hash de una secuencia igual a este subsegmento (no se requieren conversiones adicionales de grados o similares para comparar con otros valores).

Hay dos puntos a aclarar aquí:
1) Para multiplicar rápidamente por p a la potencia r-l+1, es necesario precalcular todas las potencias posibles de p módulo mod.
2) Debe recordarse que realizamos todos los cálculos módulo módulo y, por lo tanto, puede resultar que después de restar los hash del prefijo, obtengamos un número negativo. Para evitar esto, siempre puedes agregar mod antes de restar. Además, no olvide tomar el valor del módulo después de las multiplicaciones y todas las sumas.

En el código se ve así:
  #incluye <bits/stdc++.h> utilizando el espacio de nombres estándar; typedef long longll; const int MAXN = 1000003; // módulo base y hash ll p, mod; // prefijo hash y exponentes p h[MAXN], pows[MAXN]; // calculando el hash del subsegmento [l;r] ll get_segment_hash(int l, int r) { return (h[r] + mod - h[l - 1] * pows[r - l + 1] % mod) % mod; } int principal() { // de alguna manera obtener p y mod // precalcular potencias p fuerzas[0] = 1; para (int i = 0; i < MAXN; i++) pows[i] = (pows[i - 1] * p) % mod; // // solución del problema principal // devolver 0; }

Si tenemos un hash de la cadena A igual a h_A y un hash de la cadena B igual a h_B, podemos calcular rápidamente el hash de la cadena AB:
h_AB = h_A * p^|B| + h_B   <- contando todo módulo
donde |B| - la longitud de la cuerda B.

Además de secuencias, también puede codificar conjuntos. Es decir, conjuntos de objetos sin orden en ellos. Se calcula según la siguiente fórmula:
hash(A) = \(\sum_{a \in A} p^{ord(a)}\)   <- contando todo módulo
donde ord es una función que asigna a un objeto del conjunto su número ordinal absoluto entre todos los objetos posibles (por ejemplo, si los objetos son números naturales, entonces ord(x) = x, y si son letras latinas minúsculas, entonces ord(& #39;a' ;) = 1, ord('b') = 2 etc.)

Es decir, para cada objeto asociamos un valor igual a la base de la potencia del número de este objeto y sumamos todos estos valores para obtener un hash de todo el conjunto. Como se desprende claramente de la fórmula, el hash se vuelve a calcular fácilmente si se agrega o elimina un elemento del conjunto (simplemente agregue o reste el valor requerido). Misma lógica,  si no se agregan o eliminan elementos individuales, sino otros conjuntos (solo agregue / reste su hash).

Como ya puede comprender, los elementos individuales se consideran conjuntos de tamaño 1, para los cuales podemos calcular el hash. Y los conjuntos más grandes son simplemente una unión de tales conjuntos individuales, donde al combinar conjuntos, agregamos sus valores hash.

De hecho, sigue siendo el mismo hash polinomial, pero antes del coeficiente en p^m , teníamos el valor del elemento de secuencia bajo el número n - m - 1 (donde n es la longitud de la secuencia), y ahora este es el número de elementos en el conjunto cuyo número ordinal absoluto es igual a m.

En dicho hash, se debe tomar una base suficientemente grande (más grande que el tamaño máximo del conjunto) o usar hash doble para evitar situaciones en las que un conjunto de p objetos con un número ordinal absoluto m tenga el mismo hash que un conjunto con un objeto con valor absoluto. número ordinal m+1.
 

También hay varias formas de hacer hash eficiente de árboles enraizados. 
Uno de estos métodos se organiza de la siguiente manera:
Procesamos los vértices recursivamente, en orden de recorrido en profundidad. Supondremos que el hash de un solo vértice es igual a p. Para los vértices con hijos, primero ejecutamos el algoritmo para ellos, luego, a través de los hijos, calcularemos el hash del subárbol actual. Para hacer esto, considere los hash de subárboles de niños como una secuencia de números y calcule el hash a partir de esta secuencia. Este será el hash del subárbol actual.
Si el orden de los hijos no es importante para nosotros, entonces, antes de calcular el hash, clasificamos la secuencia de hash de los subárboles secundarios y luego calculamos el hash de la secuencia ordenada.

De esta manera, puede verificar el isomorfismo de los árboles: solo cuente el hash sin orden en los niños (es decir, cada vez que clasifique los hash de los niños). Y si los valores hash de las raíces coinciden, entonces los árboles son isomorfos, de lo contrario no.

Para árboles sin raíz, todo sucede de manera similar, pero el centroide debe tomarse como la raíz. O considere un par de hashes si hay dos centroides.