Module: (جاوا) زیربرنامه ها. بازگشت.


Problem

5/10

بازگشت و تکرار

Theory Click to read/hide

برای درک بازگشت، باید بازگشت را درک کنید...
 
تکرار در برنامه نویسی — به معنای وسیع — سازماندهی پردازش داده، که در آن اقدامات چندین بار تکرار می‌شوند، بدون اینکه منجر به تماس با خودشان شوند (برخلاف  %BA%D1%83%D1%80%D1%81%D0%B8%D1%8F" title="Recursion" > بازگشت). به معنای محدود — فرآیند پردازش چرخه ای داده یک مرحله ای. 
اغلب الگوریتم های تکرار شونده در مرحله جاری (تکرار) از نتیجه عملیات یا عمل مشابه محاسبه شده در مراحل قبلی استفاده می کنند.  یک مثال از این محاسبات، محاسبه روابط تکراری است. 
یک مثال ساده از یک مقدار بازگشتی فاکتوریل است: \(N!=1 \cdot 2 \cdot 3 \cdot \ ... \ \cdot N\) محاسبه مقدار در هر مرحله (تکرار) \(N=N \cdot i\) است.  هنگام محاسبه مقدار \(N\)، مقدار ذخیره شده از قبل \(N\).< br />
فاکتوریل یک عدد را می توان با استفاده از فرمول بازگشتی نیز توصیف کرد:



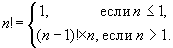
ممکن است متوجه شوید که این توضیحات چیزی بیش از یک تابع بازگشتی نیست.
در اینجا خط اول (\(n <= 1\)) — این حالت پایه (شرط پایان بازگشت) و خط دوم انتقال به مرحله بعدی است. 
  <بدن>
یک تابع فاکتوریل بازگشتی به این شکل خواهد بود مقایسه الگوریتم برای یافتن فاکتوریل به روش معمول غیر بازگشتی
int Factorial(int n){ اگر (n > 1) return n * Factorial(n - 1); else بازگشت 1; } x = 1; برای (i = 2; i <= n; i++) x = x * i; printf("%d",x);

باید درک شود که فراخوانی تابع شامل مقداری سربار اضافی است، بنابراین یک محاسبه فاکتوریل غیر بازگشتی کمی سریعتر خواهد بود. 
نتیجه گیری:جایی که می توانید یک برنامه را با یک الگوریتم تکراری ساده و بدون بازگشت بنویسید، پس باید بدون بازگشت بنویسید. اما با این حال، دسته بزرگی از مشکلات وجود دارد که در آن فرآیند محاسباتی تنها با استفاده از بازگشت اجرا می شود.
از سوی دیگر، الگوریتم های بازگشتی اغلب قابل درک تر هستند.
 

Problem

 یک تابع K(n) تعریف کنید که تعداد ارقام یک عدد طبیعی معین را برمی گرداند n: 


یک تابع بازگشتی برای محاسبه تعداد ارقام یک عدد طبیعی n بنویسید.

time 1000 ms
memory 32 Mb
Rules for program design and list of errors in automatic problem checking

Teacher commentary

Insert the missing code snippets
Java
Write the program below 
import java.util.Scanner;
public class Main {

static int CountDigit(int n)
{          
return 1+CountDigit(n/10);
}

public static void main(String[] args) {
     Scanner in = new Scanner(System.in);
     int n;
     n = in.nextInt();
     System.out.println(CountDigit(n));
   }      
}

     

Program check result

To check the solution of the problem, you need to register or log in!