درج مرتب سازی
مرتبسازی درج (مرتبسازی درج) — الگوریتم مرتبسازی که در آن عناصر دنباله ورودی یکی یکی جستجو میشوند و هر عنصر ورودی جدید در مکان مناسبی در میان عناصر مرتبسازی شده قبلی قرار میگیرد.
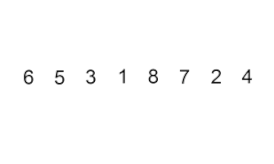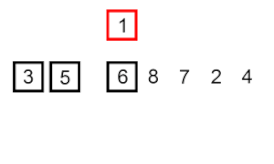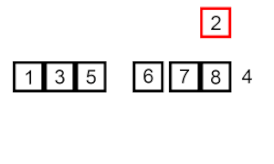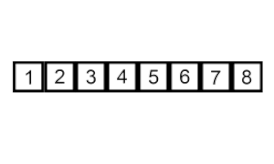
درج مرتبسازی – این یک الگوریتم بسیار ساده اما ناکارآمد است که با این وجود چندین مزیت خاص دارد که آن را حتی پس از توسعه بسیاری از الگوریتمهای کارآمدتر دیگر مرتبط میسازد.
با مرتبسازی درج، لازم نیست قبل از مرتبسازی کل آرایه را در جلو داشته باشید. الگوریتم می تواند در زمان مرتب سازی یک عنصر را دریافت کند. اگر بخواهیم عناصر بیشتری را در حین مرتبسازی اضافه کنیم، بسیار مفید است. الگوریتم عنصر جدید را بدون "اجرای مجدد" در جای مناسب وارد می کند مرتب سازی کل آرایه.
مرتبسازی درج به دلیل کارایی آن در مجموعه دادههای کوچک (~10 عنصر) در عمل قابل استفاده است.
مشکل اینجاست: بخشی از آرایه وجود دارد که از قبل مرتب شده است، و شما می خواهید با حفظ نظم، عناصر باقیمانده آرایه را در قسمت مرتب شده وارد کنید. برای انجام این کار، در هر مرحله از الگوریتم، یکی از عناصر داده ورودی را انتخاب می کنیم و آن را در محل مورد نظر در قسمت مرتب شده قبلی آرایه قرار می دهیم تا کل مجموعه داده ورودی مرتب شود. روش انتخاب عنصر بعدی از آرایه ورودی دلخواه است، اما معمولا (و برای به دست آوردن یک الگوریتم مرتبسازی پایدار)، عناصر به ترتیب ظاهرشان در آرایه ورودی درج میشوند.
اجرای الگوریتمی این الگوریتم
<پیش>
// عنصر تهی به عنوان یک دنباله از قبل مرتب شده در نظر گرفته می شود.
// بنابراین، حلقه از 1 شروع می شود
حلقه FOR I=1 به N-1 مرحله 1
X=A[I]
J=I
WHEN J>0 AND A[J-1]>X //به دنبال مکانی برای قرار دادن
EXCHANGE A[J]،A[J-1]
J=J-1
پایان خداحافظ
A[J]=X
بعدی منم
پیچیدگی محاسباتی:
\(\displaystyle O(n^{2})\).