Exemple d'arbre couvrant minimal dans un graphique avec des poids d'arête spécifiés :
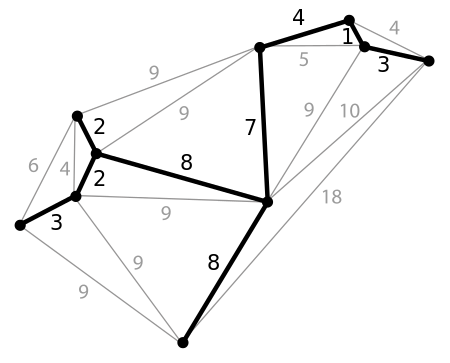
Algorithme de Kruskal :
1) Trier les bords par poids par ordre non décroissant.
2) On forme une liste de n arbres (chaque sommet est un arbre).
3) Nous commençons le processus de combinaison de ces arbres dans un arbre couvrant minimum :
toutes les arêtes sont traversées, et si les extrémités de l'arête actuelle appartiennent à des sous-arbres différents, alors ces sous-arbres sont fusionnés.
4) À la fin de l'énumération de toutes les arêtes, tous les sommets appartiendront au même sous-arbre.