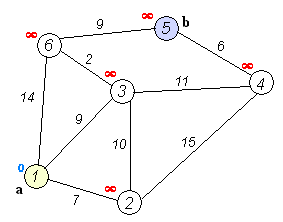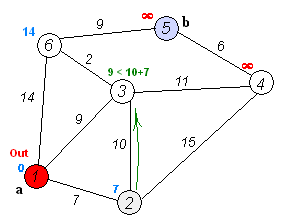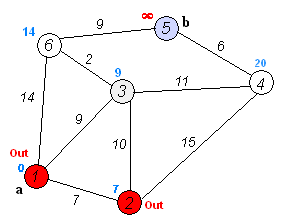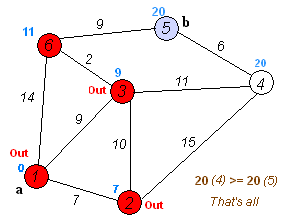
Étant donné un graphe pondéré orienté ou non orienté avec n sommets et m arêtes. Les poids de toutes les arêtes sont non négatifs. Un sommet de départ s est spécifié. Vous devez trouver les longueurs des chemins les plus courts du sommet s à tous les autres sommets, et également fournir un moyen d'imprimer les chemins les plus courts eux-mêmes.
Ce problème est appelé "problème du chemin le plus court à source unique" (problème des chemins les plus courts à source unique).
Effectue les mêmes tâches que 1-K BFS, mais sans tenir compte de K. De plus, comme 1-K BFS, il ne gère pas correctement les fronts négatifs
Algorithme :
L'algorithme de Dijkstra lui-même se compose de N itérations. A l'itération suivante, le sommet V avec la plus petite distance à lui parmi les sommets non encore marqués, ce sommet devient marqué et les relaxations des sommets voisins se produisent à partir de lui.
le comportement asymptotique final de l'algorithme est : O(n
2+ m)