Problem
Requis pour déterminer si une séquence de nombres peut être triée à l'aide d'une pile.
Un train est arrivé au cul-de-sac depuis la voie 1 (voir photo). Il est permis de décrocher une ou plusieurs premières voitures du train à la fois et de les amener dans une impasse (si vous le souhaitez, vous pouvez même amener le train entier dans une impasse en une seule fois). Après cela, amenez quelques wagons sur le côté de la voie 2. Ensuite, vous pouvez amener quelques wagons supplémentaires dans l'impasse et transporter à nouveau une partie des wagons sur le côté de la voie 2. Et ainsi de suite, de sorte que chaque wagon conduit de la voie 1 à l'impasse une seule fois, puis une fois sorti de l'impasse sur la voie 2. L'entrée dans l'impasse depuis la voie 2 ou la sortie de l'impasse sur la voie 1 est interdite. Vous ne pouvez pas passer du chemin 1 au chemin 2 sans entrer dans une impasse.
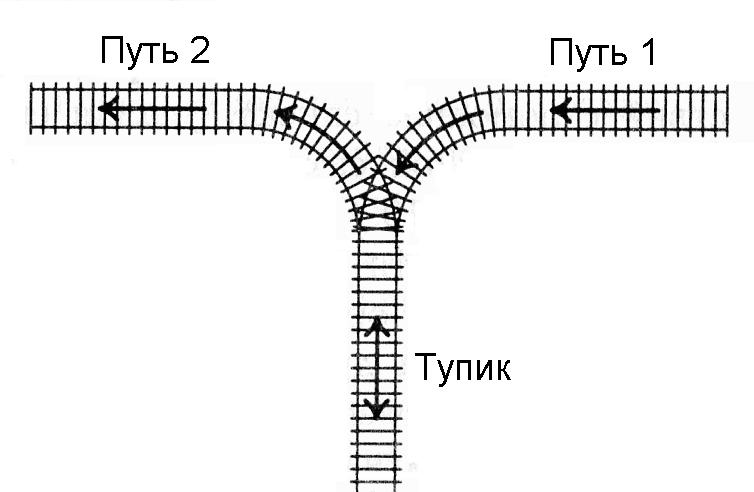
On sait dans quel ordre les wagons vont initialement. Il est nécessaire, en utilisant les opérations indiquées, de faire avancer les wagons du train dans l'ordre (d'abord le premier, puis le second, etc., en partant de la tête du train circulant sur la voie 2 en s'éloignant de l'impasse). Écrivez un programme pour déterminer si cela peut être fait.
Entrée
Entrez le numéro N — le nombre de wagons dans le train (\(1<=N<=2000\)). Viennent ensuite les numéros de voiture dans l'ordre depuis la tête du train circulant sur la voie 1 vers l'impasse. Les voitures sont numérotées avec des nombres naturels de 1 à N, chacun d'eux se produisant exactement une fois.
Sortie
Est-il possible de faire passer les wagons dans l'ordre de 1 à N, en partant de la tête du train, lorsque le train emprunte la voie 2 depuis l'impasse ? Si possible, affichez un message OUI. Si ce n'est pas possible, écrivez NON.
Exemples
| # |
Entrée |
Sortie |
Remarque |
| 1 |
3
3 2 1
| OUI |
Nous devons amener tout le train dans une impasse, puis le conduire entièrement jusqu'à la 2ème voie |
| 2 |
4
4 1 3 2
OUI
Tout d'abord, vous devez amener deux wagons dans une impasse, dont l'un sera laissé dans une impasse, et le second — sortez sur la 2ème piste, puis amenez deux autres voitures dans l'impasse et sortez 3 voitures se tenant à l'impasse sur la 2ème piste |
| 3 |
3
2 3 1
| NON |
|