Au lieu de simplement calculer le hachage d'une séquence, nous pouvons stocker la valeur à chacun de ses préfixes. Notez qu'il s'agira de valeurs de hachage pour les séquences égales au préfixe correspondant.
Avec une telle structure, vous pouvez rapidement calculer la valeur de hachage pour n'importe quel sous-segment de cette séquence (similaire aux sommes de préfixes).
Si nous voulons calculer le hachage du sous-segment [l;r], alors nous devons prendre le hachage sur le préfixe r et soustraire le hachage sur le préfixe l-1 multiplié par p à la puissance r-l+1. Pourquoi il en est ainsi devient clair si vous écrivez les valeurs sur les préfixes et voyez ce qui se passe. J'espère que vous réussirez à regarder cette photo.
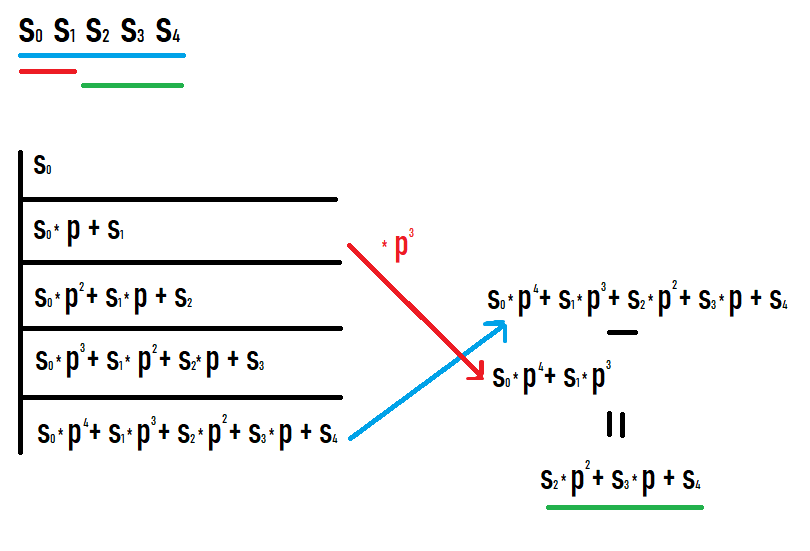
À la suite de telles actions, nous obtenons un hachage d'un sous-segment de la séquence d'origine. De plus, ce hachage est égal à celui s'il était considéré comme un hachage d'une séquence égale à ce sous-segment (aucune conversion supplémentaire de degrés ou similaire n'est requise pour comparer avec d'autres valeurs).
Il y a deux points à clarifier ici :
1) Pour multiplier rapidement par p à la puissance r-l+1, il faut précalculer toutes les puissances possibles de p modulo mod.
2) Il faut se rappeler que nous effectuons tous les calculs modulo modulo, et donc il peut s'avérer qu'après avoir soustrait les hachages de préfixe, nous obtiendrons un nombre négatif. Pour éviter cela, vous pouvez toujours ajouter un mod avant de soustraire. Aussi, n'oubliez pas de prendre la valeur modulo après multiplications et toutes additions.
Dans le code, cela ressemble à ceci :
#include <bits/stdc++.h>
en utilisant l'espace de noms std ;
typedef long longll ;
const entier MAXN = 1000003 ;
// module de base et de hachage
ll p, mod;
// préfixe hachage et exposants p
h[MAXN], pows[MAXN] ;
// calcul du hash du sous-segment [l;r]
ll get_segment_hash(int l, int r) {
retour (h[r] + mod - h[l - 1] * pows[r - l + 1] % mod) % mod ;
}
int main()
{
// obtenir en quelque sorte p et mod
// précalcule les puissances p
pows[0] = 1 ;
pour (int i = 0; je < MAXN; i++)
pows[i] = (pows[i - 1] * p) % mod ;
//
// solution du problème principal
//
renvoie 0 ;
}