Insérer un tri
Tri par insertion (Tri par insertion) — ;algorithme de tri dans lequel les éléments de la séquence d'entrée sont recherchés un par un, et chaque nouvel élément entrant est placé à l'endroit approprié parmi les éléments précédemment triés.
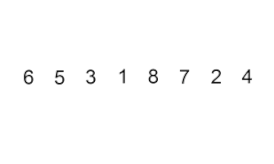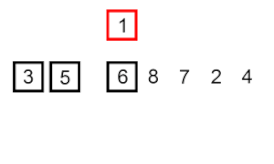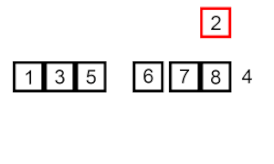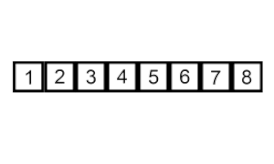
Insérer le tri – c'est un algorithme très simple mais peu efficace qui présente néanmoins plusieurs avantages spécifiques qui le rendent pertinent même après que de nombreux autres algorithmes généralement plus efficaces aient été développés.
Avec le tri par insertion, vous n'avez pas besoin d'avoir tout le tableau devant vous avant le tri. L'algorithme peut recevoir un élément à la fois lors du tri. Ceci est très pratique si nous devons ajouter plus d'éléments lors du tri. L'algorithme insérera le nouvel élément au bon endroit sans "ré-exécuter" trier l'ensemble du tableau.
Le tri par insertion peut être utilisé en pratique en raison de son efficacité sur de petits ensembles de données (~10 éléments).
Le problème est le suivant : une partie du tableau est déjà triée et vous souhaitez insérer les éléments restants du tableau dans la partie triée, tout en maintenant l'ordre. Pour ce faire, à chaque étape de l'algorithme, nous sélectionnons l'un des éléments de données d'entrée et l'insérons à la position souhaitée dans la partie déjà triée du tableau, jusqu'à ce que l'ensemble des données d'entrée soit trié. La méthode de sélection de l'élément suivant dans le tableau d'entrée est arbitraire, mais généralement (et afin d'obtenir un algorithme de tri stable), les éléments sont insérés dans l'ordre de leur apparition dans le tableau d'entrée.
Implémentation algorithmique de cet algorithme
// L'élément nul est considéré comme une séquence déjà triée.
// Par conséquent, la boucle commence à partir de 1
BOUCLE POUR I=1 VERS N-1 ETAPE 1
X=A[Je]
J=je
QUAND J>0 ET A[J-1]>X //recherche un endroit pour insérer
ÉCHANGE A[J],A[J-1]
J=J-1
FIN AU REVOIR
A[J]=X
ENSUITE JE
Complexité de calcul : \(\displaystyle O(n^{2})\).