sous-programmes. récursivité

Une procédure ou une fonction peut contenir un appel à une autre procédure en son sein. Y compris, le sous-programme peut s'appeler. Dans ce cas, l'ordinateur s'en fiche. Il exécute également, comme toujours, systématiquement les commandes qu'il a rencontrées de haut en bas.

Si vous vous souvenez des mathématiques, vous pouvez y rencontrer le principe d'induction mathématique. C'est comme suit :

Une certaine affirmation est vraie pour chaque natureln si
    1. il est valable pour n = 1 et
    2. de la validité de l'énoncé pour tout naturel arbitraire n = k il s'ensuit qu'il est vrai pourn = k+1.

En programmation, cette technique est appelée récursivité

La récursivité est un moyen de définir un ensemble d'objets en fonction de l'ensemble lui-même, sur la base de cas de base simples donnés.

Récursif sera également appelé une procédure (fonction) qui s'appelle elle-même directement ou via d'autres procédures et fonctions
Un exemple de procédure récursive : procédure Rec(a : entier); commencer     si un > 0 alors         Rec(a - 1);     écrire un); fin ; Schématiquement, le travail de récursivité peut être représenté par un organigramme

 

La procédure Rec() est exécutée avec le paramètre 3. Ensuite, à l'intérieur de la procédure avec le paramètre 3, la procédure avec le paramètre 2 est appelée, et ainsi de suite, jusqu'à ce que la procédure avec le paramètre 0 soit appelée. Lorsque la procédure avec le paramètre le paramètre 0 est appelé, l'appel récursif ne se produira déjà pas et la procédure avec le paramètre 0 imprimera le numéro 0 et se terminera. Ensuite, le contrôle est renvoyé à la procédure avec le paramètre 1, elle termine également son travail en imprimant le numéro 1, et ainsi de suite. avant la procédure avec le paramètre 3. 

Toutes les procédures appelées sont stockées en mémoire jusqu'à ce qu'elles terminent leur travail. Le nombre de procédures concurrentes est appelé profondeur de récursivité.

Nous avons vu que la récursivité est l'exécution répétée d'instructions contenues dans un sous-programme. Et cela, à son tour, est similaire au travail du cycle. Il existe des langages de programmation dans lesquels la construction de boucle est absente du tout, par exemple Prolog. 
Essayons de simuler le fonctionnement de la boucle for. 
La boucle for contient une variable de compteur de pas. Dans un sous-programme récursif, une telle variable peut être passée en paramètre. //Procédure LoopImitation() avec deux paramètres //Premier paramètre – compteur de pas, second paramètre – nombre total d'étapes procédure LoopImitation(i, n : entier); commencer     writeln('Bonjour N', je); // Opérateur à répéter pour toute valeur de i     si je < n then //Jusqu'à ce que le compteur de boucle devienne égal à la valeur n,         BoucleImitation(i + 1, n); //appel d'une nouvelle instance de la procédure, avec le paramètre i+1 (passage à la valeur suivante i) fin;

Itération dans la programmation — au sens large — organisation du traitement des données, dans laquelle les actions sont répétées plusieurs fois, sans conduire à des appels à elles-mêmes (contrairement à Récursions). Au sens étroit — processus de traitement de données cyclique en une étape. 
Souvent, les algorithmes itératifs à l'étape en cours (itération) utilisent le résultat de la même opération ou action calculée aux étapes précédentes.  Un exemple de tels calculs est le calcul des relations de récurrence. 
Un exemple simple de valeur de récurrence est la factorielle : \(N!=1 \cdot 2 \cdot 3 \cdot \ ... \ \cdot N\) Le calcul de la valeur à chaque étape (itération) est \(N=N \cdot i\) .  Lors du calcul de la valeur de \(N\), nous prenons la valeur déjà stockée\(N\).< br />
La factorielle d'un nombre peut également être décrite à l'aide de la formule récurrente :



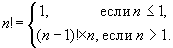
Vous remarquerez peut-être que cette description n'est rien de plus qu'une fonction récursive.
Ici la première ligne (\(n <= 1\)) — c'est le cas de base (condition de fin de récursivité) et la deuxième ligne est la transition vers l'étape suivante. 
 

Une fonction factorielle récursive ressemblerait à ceci	Comparez l'algorithme pour trouver la factorielle de la manière habituelle et non récursive
fonction Factorielle(n : entier) : entier ; commencer     si n > 1 puis         Factorielle := n * Factorielle(n - 1)     sinon         Factoriel := 1; fin;	x := 1; pour i := 2 à n faire     x := x * je; écrireln(x);

Il faut comprendre que les appels de fonction impliquent une surcharge supplémentaire, donc un calcul factoriel non récursif sera légèrement plus rapide. 
Conclusion : où vous pouvez écrire un programme avec un algorithme itératif simple, sans récursivité, alors vous devez écrire sans récursivité. Mais encore, il existe une grande classe de problèmes où le processus de calcul est mis en œuvre uniquement par récursivité.
En revanche, les algorithmes récursifs sont souvent plus compréhensibles.