निर्दिष्ट किनारे भार वाले ग्राफ़ में न्यूनतम फैले हुए पेड़ का एक उदाहरण:
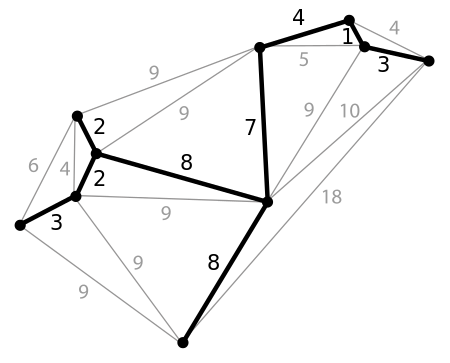
क्रुस्कल का एल्गोरिद्म:
1) वजन के अनुसार किनारों को छाँटें गैर-घटते क्रम में।
2) हम n पेड़ों की एक सूची बनाते हैं (प्रत्येक शीर्ष एक पेड़ है)।
3) हम इन पेड़ों को न्यूनतम फैले हुए पेड़ में संयोजित करने की प्रक्रिया शुरू करते हैं:
सभी किनारों को पार किया जाता है, और यदि वर्तमान किनारे के सिरे अलग-अलग सबट्री से संबंधित हैं, तो ये सबट्री मर्ज हो जाते हैं।
4) सभी किनारों की गणना के अंत में, सभी कोने एक ही सबट्री से संबंधित होंगे।