Module: (जावा) सबरूटीन्स। पुनरावर्तन।


Problem

5/10

पुनरावर्तन और पुनरावृत्ति

Theory Click to read/hide

रिकर्सन को समझने के लिए, आपको रिकर्सन को समझने की जरूरत है...
 
<कोड>पुनरावृत्ति प्रोग्रामिंग में — व्यापक अर्थों में — डेटा प्रोसेसिंग का संगठन, जिसमें कार्रवाइयाँ कई बार दोहराई जाती हैं, बिना खुद को कॉल किए (विपरीत  %BA%D1%83%D1%80%D1%81%D0%B8%D1%8F" title="Recursion" >पुनरावृत्ति)। संकीर्ण अर्थ में — एक चरण चक्रीय डेटा संसाधन प्रक्रिया। 
वर्तमान चरण (पुनरावृत्ति) पर अक्सर पुनरावृत्त एल्गोरिदम पिछले चरणों में गणना किए गए समान ऑपरेशन या क्रिया के परिणाम का उपयोग करते हैं।  ऐसी गणनाओं का एक उदाहरण पुनरावृत्ति संबंधों की गणना है। 
पुनरावर्ती मान का एक सरल उदाहरण भाज्य है: \(N!=1 \cdot 2 \cdot 3 \cdot \ ... \ \cdot N\) प्रत्येक चरण (पुनरावृत्ति) पर मूल्य की गणना \(N=N \cdot i\) है।  \(N\) के मान की गणना करते समय, हम पहले से संग्रहीत मान लेते हैं \(N\)।< बीआर />
किसी संख्या के क्रमगुणन को पुनरावर्ती सूत्र:
का उपयोग करके भी वर्णित किया जा सकता है


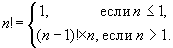
आप देख सकते हैं कि यह विवरण एक पुनरावर्ती क्रिया से अधिक कुछ नहीं है।
यहाँ पहली पंक्ति (\(n <= 1\)) — यह आधार मामला है (पुनरावृत्ति की अंतिम स्थिति) और दूसरी पंक्ति अगले चरण के लिए संक्रमण है। 
  <तालिका सीमा = "1" सेलपैडिंग = "1" सेलस्पेसिंग = "1" शैली = "चौड़ाई: 500 पीएक्स"> <शरीर> रिकर्सिव फैक्टोरियल फंक्शन इस तरह दिखेगा सामान्य गैर-पुनरावर्ती तरीके से फैक्टोरियल खोजने के लिए एल्गोरिदम की तुलना करें <टीडी> इंट फैक्टोरियल (इंट एन) { अगर (एन एंड जीटी; 1) रिटर्न एन * फैक्टोरियल (एन - 1); और वापसी 1; } <टीडी> एक्स = 1; के लिए (i = 2; i <= n; i++) एक्स = एक्स * मैं; प्रिंटफ("%d",x);
यह समझा जाना चाहिए कि फ़ंक्शन कॉल में कुछ अतिरिक्त ओवरहेड शामिल होते हैं, इसलिए एक गैर-पुनरावर्ती फैक्टोरियल गणना थोड़ी तेज़ होगी। 
निष्कर्ष: जहां आप एक सरल पुनरावृत्ति एल्गोरिथ्म के साथ एक कार्यक्रम लिख सकते हैं, बिना पुनरावर्तन के, तो आपको बिना पुनरावर्तन के लिखने की आवश्यकता है। लेकिन फिर भी, समस्याओं का एक बड़ा वर्ग है जहाँ कम्प्यूटेशनल प्रक्रिया केवल पुनरावर्तन द्वारा कार्यान्वित की जाती है।
दूसरी ओर, पुनरावर्ती एल्गोरिदम अक्सर अधिक समझने योग्य होते हैं।
 

Problem

 ऐसे फ़ंक्शन को परिभाषित करें K(n) जो किसी दिए गए प्राकृतिक नंबर n में अंकों की संख्या लौटाता है: 


प्राकृतिक संख्या n में अंकों की संख्या की गणना के लिए एक पुनरावर्ती कार्य लिखें।

time 1000 ms
memory 32 Mb
Rules for program design and list of errors in automatic problem checking

Teacher commentary

Insert the missing code snippets
Java
Write the program below 
import java.util.Scanner;
public class Main {

static int CountDigit(int n)
{          
return 1+CountDigit(n/10);
}

public static void main(String[] args) {
     Scanner in = new Scanner(System.in);
     int n;
     n = in.nextInt();
     System.out.println(CountDigit(n));
   }      
}

     

Program check result

To check the solution of the problem, you need to register or log in!