Module: दिज्क्स्ट्रा का एल्गोरिथ्म


Problem

1/14

दिज्क्स्ट्रा: द बिगिनिंग (C++)

Theory Click to read/hide

<दिव>

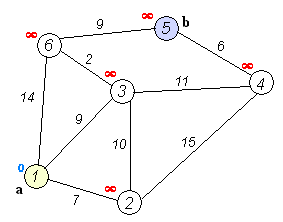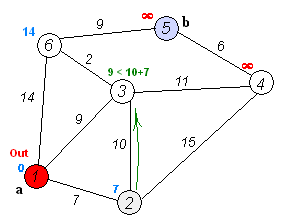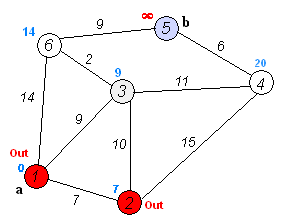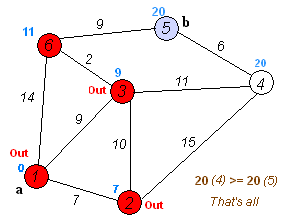
एन वर्टिकल और एम किनारों के साथ एक निर्देशित या अप्रत्यक्ष भारित ग्राफ दिया गया है। सभी किनारों का भार गैर-ऋणात्मक है। कुछ आरंभिक शीर्ष निर्दिष्ट किए गए हैं। आपको शीर्ष s से अन्य सभी शीर्षों तक सबसे छोटे पथों की लंबाई ज्ञात करने की आवश्यकता है, और स्वयं सबसे छोटे पथों को प्रिंट करने का तरीका भी प्रदान करें।
 
इस समस्या को "एकल स्रोत सबसे छोटी पथ समस्या" कहा जाता है (एकल-स्रोत लघुतम पथ समस्या)।

1-के बीएफएस के समान कार्य करता है, लेकिन के पर ध्यान दिए बिना। साथ ही, 1-के बीएफएस की तरह, यह नकारात्मक किनारों को ठीक से नहीं संभालता है

एल्गोरिदम:
दिज्क्स्त्र के एल्गोरिद्म में ही N पुनरावृत्तियां हैं। अगले पुनरावृति पर, शीर्ष V  अभी तक चिह्नित नहीं किए गए शीर्षों में से इसकी सबसे छोटी दूरी के साथ, यह शीर्ष चिह्नित हो जाता है और इससे पड़ोसी शीर्षों की छूट मिलती है।


 एल्गोरिदम का अंतिम स्पर्शोन्मुख व्यवहार है: O(n2+ m)

Problem

आपको एक निर्देशित भारित ग्राफ दिया जाता है। एक दिए गए शीर्ष से दूसरे शीर्ष तक की न्यूनतम दूरी ज्ञात कीजिए।
 
इनपुट
पहली पंक्ति में तीन संख्याएँ हैं: N, S और F (1≤ N≤ 100, 1≤ S, F≤ N), जहाँ N – ग्राफ़ शीर्षों की संख्या, S – आरंभिक शीर्ष, और F – अंतिम। अगली एन पंक्तियों में, प्रत्येक संख्या एन संख्या दर्ज करें, 100 से अधिक नहीं, – ग्राफ़ का भार आसन्न मैट्रिक्स, जहाँ -1 का अर्थ है शीर्षों के बीच कोई किनारा नहीं, और कोई भी गैर-ऋणात्मक संख्या – दिए गए वजन के किनारे की उपस्थिति। मैट्रिक्स के मुख्य विकर्ण पर शून्य लिखे जाते हैं।
 
आउटपुट
वांछित दूरी प्रदर्शित करना आवश्यक है या -1 यदि निर्दिष्ट शीर्षों के बीच कोई पथ नहीं है।

उदाहरण <टेबल क्लास = "टेबल टेबल-कंडेंस्ड टेबल-होवर"> <सिर> <वें># <वें>इनपुट <वें>आउटपुट <शरीर> 1 <टीडी>
3 2 1
0 1 1
4 0 1
2 1 0
3

time 1000 ms
memory 32 Mb
Rules for program design and list of errors in automatic problem checking

Teacher commentary

Insert the missing code snippets
C++
Write the program below 
#include<iostream>
 
using namespace std;
 
int main()
{
    const int N1 = 110;
    int N, S, F, g[N1][N1], i, j, mini, d[N1];
    bool used[N1];
   
    cin >> N >> S >> F;
   
    fill(used, used + N, false);
   
    fill(d, d + N, 10000000);
   
    for (i = 0; i < N; i++)
    {
        for (j = 0; j < N; j++)
            cin >> g[i][j];
    }
   
    d[S - 1] = 0;
   
    for (i = 0; i < N; i++)
    {
        mini = -1;
       
        for (j = 0; j < N; j++)
        {
            if (!used[j] && (mini == -1 || d[j] < d[mini]))
                mini = j;
        }
       
        used[mini] = true; 
    if (d[F - 1] == 10000000)
        cout << "-1";
    else
        cout << d[F - 1];
}

     

Program check result

To check the solution of the problem, you need to register or log in!