Problem

2/6

बीएफएस: शुरुआत (पायथन)

Theory Click to read/hide

बीएफएस (चौड़ाई-पहली खोज) एक ग्राफ ट्रैवर्सल विधि है, जो अक्सर सरल और उन्नत एल्गोरिदम दोनों में उपयोग की जाती है। ब्रेड्थ-फर्स्ट सर्च ग्राफ़ के अलग-अलग स्तरों के माध्यम से काम करता है, स्रोत नोड से शुरू होता है और धीरे-धीरे इससे दूर हो जाता है। यह एनीमेशन में स्पष्ट रूप से दिखाया गया है।

>
एक साधारण बीएफएस लिखने के लिए, आपको कतार के साथ काम करने में सक्षम होना चाहिए, एक डेटा संरचना जो आपको शुरू से लेने और इसे अंत तक रखने की अनुमति देती है, और फॉर्म में एक ग्राफ को स्टोर करने में भी सक्षम है। निकटता सूची की।
 
एल्गोरिदम का औपचारिक विवरण
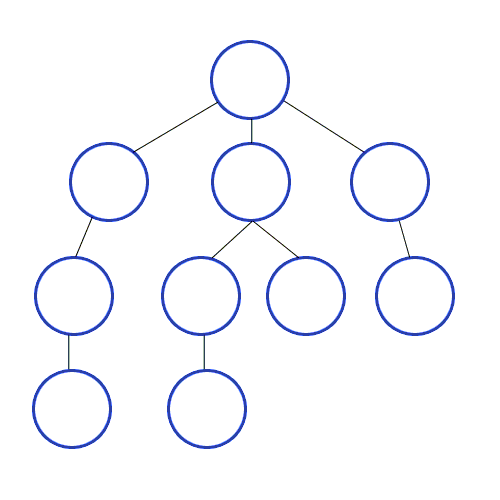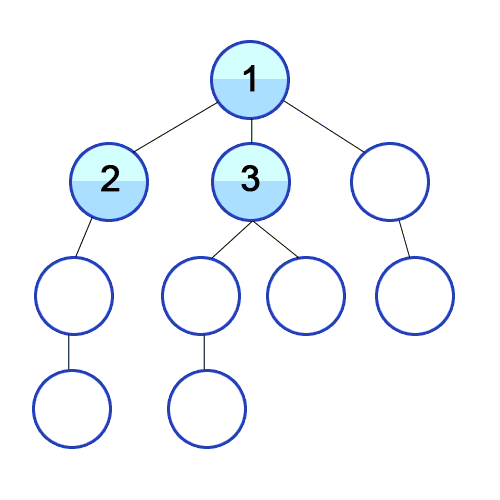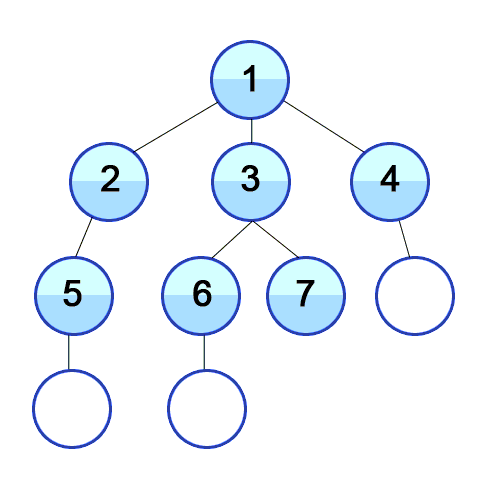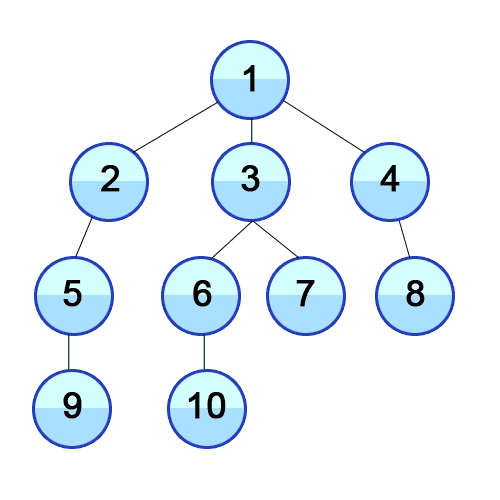
1) शुरुआती खाली कतार में उस शीर्ष की संख्या डालें जहां से खोज शुरू होती है।
2) कतार की शुरुआत से वर्टेक्स यू निकालें और इसे एक अलग सरणी में उपयोग के रूप में चिह्नित करें।
3) कतार के अंत में, उन सभी शीर्षों को जोड़ें, जिन तक हम शीर्ष U से किनारे का उपयोग करके पहुंच सकते हैं और जो अभी तक चिह्नित नहीं हैं।
4) यदि कतार खाली है, तो जुड़े हुए ग्राफ़ के सभी नोड्स स्कैन किए गए हैं, अन्यथा चरण 2 पर वापस लौटें।
 
काम में कठिनाई
चूंकि, सबसे खराब स्थिति में, एल्गोरिथ्म ग्राफ के सभी नोड्स पर जाता है, जब ग्राफ को आसन्न सूचियों के रूप में संग्रहीत किया जाता है, तो एल्गोरिथ्म की समय जटिलता O(|V| + |E|) होती है, जहां V सेट होता है ग्राफ़ के शीर्षों की संख्या, और E किनारों का समूह है। ;
दूसरे शब्दों में, एल्गोरिदम किनारों की संख्या + शीर्षों की संख्या के लिए सबसे खराब स्थिति में काम करता है।

 

Problem

कुछ गांव सड़कों से जुड़े हुए हैं, जिन्हें एक अप्रत्यक्ष ग्राफ के रूप में दर्शाया जा सकता है। इस ग्राफ के कोने गाँव हैं, और किनारे गाँवों के बीच की सड़कें हैं (ग्राफ़ में चक्र हो सकते हैं)। यह ज्ञात है कि गाँव में S एक artel व्यापारी. हर सुबह, अपनी छोटी बिसाती की दुकान बेचने के लिए, फेरीवाले उन गांवों में जाते हैं जहां अभी तक नहीं गए हैं, और जहां तक वर्तमान गांव से एक सड़क है. पैडलर्स के आर्टेल को हमेशा समूहों में विभाजित किया जाता है ताकि वे एक दिन में उन सभी गांवों का चक्कर लगा सकें जहां सड़कें हैं।
फेरीवाले सभी गाँवों का दौरा कितने दिनों में करेंगे? एक \(bfs()\) फ़ंक्शन लिखें जो समस्या का उत्तर लौटाएगा।


इनपुट
पहली पंक्ति में 3 पूर्णांक होते हैं n, m, s (\(1 < = n <= 10^5\), \(0 <= m <= 10^5\), \(1 <= s <= n\)) - गांवों की संख्या, उनके बीच की सड़कों की संख्या, और उस गांव की संख्या जिसमें फेरीवालों का गिरोह स्थित है।  ;निम्नलिखित m पंक्तियों में प्रत्येक u, v(\(1 < = यू, वी <= एन\)) - दो गांवों की संख्या जिनके बीच एक सड़क है। गांवों को 1 से अनुक्रमित किया जाता है।

छाप
एक ही नंबर प्रिंट करें - सभी गांवों का दौरा करने में फेरीवालों को कितने दिन लगेंगे।
 
 
उदाहरण
<टेबल क्लास = "टेबल-बॉर्डर्ड टेबल-लिस्ट-टेस्ट टेबल-एसएम टेबल-स्ट्राइप्ड"> <सिर> <वें># <वें>इनपुट <वें>आउटपुट <शरीर> 1 6 7 1
1 2
15
23
5 4
34
36
4 6 4

time 1000 ms
memory 32 Mb
Rules for program design and list of errors in automatic problem checking

Teacher commentary

Insert the missing code snippets
Python
Write the program below 
def bfs():            
n, m, s = map(int, input().split())
s -= 1
used = [False] * n  # True, если были в вершине i
tm = [0] * n    # tm[i] - день, когда в деревню i пришла артель коробейников
g = []     # список смежности
for i in range(n):
    g.append([])


for i in range(m):
    u, v = map(int, input().split())
    u -= 1
    v -= 1
    g[u].append(v)
    g[v].append(u)

print(bfs())

     

Program check result

To check the solution of the problem, you need to register or log in!