k द्वारा n तत्वों के संयोजन यौगिक हैं जो n तत्वों से बन सकते हैं, प्रत्येक कनेक्शन में k तत्वों को एकत्रित करते हैं; जबकि कनेक्शन केवल तत्वों द्वारा एक दूसरे से भिन्न होते हैं (उनकी व्यवस्था के क्रम में अंतर को ध्यान में नहीं रखा जाता है)।
उदाहरण के लिए, निम्नलिखित संयोजन 3 तत्वों (a,b,c)(a,b,c) प्रत्येक 2 से बन सकते हैं: ab,ac,bc।
सभी संभावित संयोजनों की संख्या जो n तत्वों से k द्वारा बनाई जा सकती है, प्रतीक

और सूत्र द्वारा गणना की गई:
संयोजनों की संख्या का पता लगाने के दो तरीके हैं

1. n!, k!, (n – k) ज्ञात कीजिए! और उपरोक्त सूत्र के अनुसार, हम मात्रा की गणना करते हैं, लेकिन – संभावित अतिप्रवाह के कारण, इस विधि का उपयोग n <= 12.
के साथ किया जा सकता है
2. गतिशील प्रोग्रामिंग के साथ।
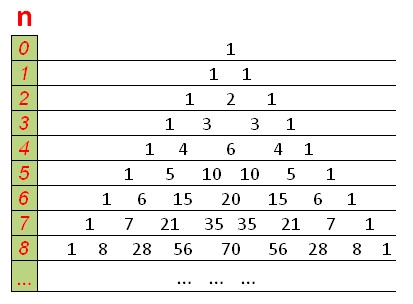
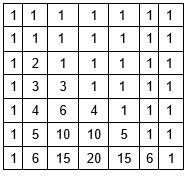
डीपी पास्कल के त्रिकोण की तरह दिखेगी, जिसमें ऊपर और किनारों पर त्रिकोण होंगे, और प्रत्येक संख्या इसके ऊपर की दो संख्याओं के योग के बराबर होगी।
एक फ़ंक्शन जो O(n ^2 ):
में गतिशील प्रोग्रामिंग का उपयोग करके संयोजनों की संख्या की गणना करता है
का उपयोग करके उत्पन्न किया गया
<पूर्व शैली = "मार्जिन-बाएं: 0 पीएक्स; मार्जिन-दाएं: 0 पीएक्स">
int C(int n, int के)
{
वेक्टर<वेक्टर<int> > dp(n + 1, वेक्टर<int>(n + 1, 1)); // आकार की एक dp सरणी बनाएं (n + 1, n + 1)
for (int i = 0; i <= n; i++) // सरणी की i-वीं पंक्ति भरें
{
for (int j = 1; j < i; j++)
{
डीपी [मैं] [जे] = डीपी [मैं - 1] [जे - 1] + डीपी [मैं - 1] [जे]; //पुनरागणना (i;j) स्थिति (i - 1; j - 1) और (i - 1; j) के माध्यम से
}
}
वापसी dp[n][k]; //रिटर्न वैल्यू
}