Module: त्रिगुट खोज

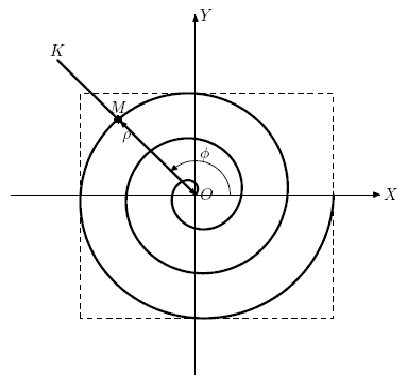
दीमा हाल ही में फ्लैट कर्व्स के अनुसंधान संस्थान में शामिल हुई हैं। जैसा कि इस शोध संस्थान के नाम से पता चलता है, यह समतल वक्रों के क्षेत्र में विभिन्न शोधों में लगा हुआ है। हाल ही में, डिमिन के बॉस जॉर्जी ने एक बहुत ही दिलचस्प वक्र का सामना किया, जो कि कुछ शोधों के बाद निकला, आर्किमिडीयन सर्पिल के रूप में जाना जाता है। आर्किमिडीयन सर्पिल एक समतल वक्र है जो बिंदु M के प्रक्षेपवक्र को दर्शाता है, जो O पर उत्पत्ति के साथ किरण OK के साथ समान रूप से चलता है, जबकि किरण OK स्वयं बिंदु O के चारों ओर समान रूप से घूमती है (चित्र देखें)। दूसरे शब्दों में, मूल बिंदु से दूरी ρ = ओम रैखिक रूप से रोटेशन के कोण पर निर्भर है। फाई। किरण ठीक। इस स्थिति में, किरण OK का उसी कोण से घूमना समान दूरी वृद्धि के अनुरूप होता है ρ 

 

बिंदु M की गति को कई मापदंडों का उपयोग करके सेट किया जा सकता है:

 

• रोटेशन का प्रारंभिक कोण। अल्फा। बीम OK (OX अक्ष की धनात्मक दिशा के सापेक्ष वामावर्त डिग्री में मापा गया);

 

• कोणीय वेग .ओमेगा। रे ओके (डिग्री प्रति समय इकाई में मापा गया);

 

• प्रारंभिक दूरी आर बिंदु एम से मूल (बिंदु ओ);

 

• किरण OK के अनुदिश बिंदु M का वेग V.

 

यदि, इन मापदंडों को सेट करके, हम बिंदु M के संचलन के समय को सीमित नहीं करते हैं, तो हमें एक अनंत वक्र मिलता है, जिसका पता लगाना काफी कठिन है। इसलिए, दीमा ने इस वक्र के कुछ हिस्से का अध्ययन करने के लिए खुद को सीमित करने का फैसला किया, वह जो तब प्राप्त होता है जब बिंदु M समय के शून्य क्षण से समय के क्षण तक चला जाता है। दीमा जिस समस्या को हल करती है वह आयत का एक आयत खोजना है। निर्देशांक अक्षों के समांतर भुजाओं वाला न्यूनतम क्षेत्र, जिसमें इसे अंकित किया जा सकता है।

 

आपको एक ऐसा प्रोग्राम लिखने की आवश्यकता है जो वांछित आयत को खोज सके

 

इनपुट फ़ाइल में चार पूर्णांक होते हैं: ω (1 ≤ ओमेगा; ≤ 100), V (1 ≤ V ≤ 100), R (0 ≤ R ≤ 100) और T (1 ≤ T≤ 1000)। इस समस्या में, यह मान लिया जाता है कि प्रारंभिक घूर्णन कोण .alpha है। शून्य है।

 

आउटपुट फ़ाइल की पहली पंक्ति में दो वास्तविक संख्याएँ प्रिंट करें — वांछित आयत के निचले बाएँ कोने के निर्देशांक, और दूसरी पंक्ति में — वांछित आयत के ऊपरी दाएं कोने के निर्देशांक।

 

उत्तर को सही माना जाएगा यदि प्रत्येक निर्देशांक का मान वास्तविक मान से 10-5 से अधिक भिन्न न हो।
  <तालिका सीमा = "1" सेलपैडिंग = "1" सेलस्पेसिंग = "1" शैली = "चौड़ाई: 500 पीएक्स"> <शरीर> इनपुट आउटपुट 60 10 0 18 <टीडी>
टीम ओलंपियाड, VKOSHP, 2008, समस्या I