Problem
आकाशगंगा में n ग्रह हैं, जिनमें से प्रत्येक में कई अलग-अलग जीवित प्राणियों का निवास है। और उनमें से प्रत्येक परेशानी में हो सकता है! अंतरिक्ष बचावकर्ता इसके बारे में अच्छी तरह से जानते हैं और हमेशा किसी की भी मदद करने के लिए तैयार रहते हैं जिन्हें वास्तव में इस मदद की जरूरत होती है। आपको बस कॉल करना है।
अंतरिक्ष बचावकर्ता अब आकाशगंगा के इतिहास में सबसे बड़ा बचाव आधार बनाने की योजना बना रहे हैं, लेकिन भविष्य के आधार का स्थान अभी तक निर्धारित नहीं किया गया है। चूँकि मदद की कभी-कभी तत्काल आवश्यकता होती है, इसलिए बचावकर्ता आकाशगंगा में एक बिंदु खोजने का प्रयास करते हैं जहाँ से कम से कम समय में सबसे दूर के ग्रह तक पहुँचना संभव होगा। दूसरे शब्दों में, अंतरिक्ष में ऐसे बिंदु को खोजना आवश्यक है ताकि उससे सबसे दूर के ग्रह की दूरी अंतरिक्ष में सभी संभावित बिंदुओं में सबसे छोटी हो। दुर्भाग्य से, वे ऐसी समस्या को हल करने में असमर्थ हैं।
चूंकि ग्रह काफी दूर हैं, उन्हें यूक्लिडियन 3डी अंतरिक्ष में बिंदुओं के रूप में माना जा सकता है। बिंदुओं के बीच की दूरी (x
i, y
i, z
i) और (x
j, y
j, z
j) की गणना सूत्र द्वारा की जाती है:
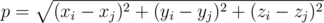
बचाव आधार अंतरिक्ष में किसी भी बिंदु पर स्थित हो सकता है, जिसमें किसी भी ग्रह के साथ संयोग शामिल है।
आकाशगंगा खतरे में है! अंतरिक्ष बचावकर्मियों को बचाएं और उन्हें वांछित बिंदु पर इंगित करें।
इनपुट
इनपुट फ़ाइल की पहली पंक्ति में एक पूर्णांक n — ग्रहों की संख्या (1 ≤ N ≤ 100)। अगली n पंक्तियों में से प्रत्येक में ग्रहों के बारे में जानकारी है। इन पंक्तियों के i-वें में तीन पूर्णांक हैं xi, yi, zi — i-वें ग्रह निर्देशांक ( - 104 ≤ xi, yi, zi ≤ 104, 1.thinsp;≤ i ≤ n)। कोई भी दो ग्रह एक जैसे नहीं होते।
आउटपुट
आउटपुट फ़ाइल की पहली पंक्ति में, स्पेस से अलग तीन वास्तविक संख्याएँ x
0, y
0, z
0 — आधार निर्देशांक। यदि कई समाधान हैं, तो किसी एक को प्रिंट करने की अनुमति है। उत्तर गिना जाएगा यदि इस बिंदु से सबसे दूर के ग्रह की दूरी जूरी के परिणाम से पूर्ण या सापेक्ष मूल्य में 10-6 से अधिक भिन्न नहीं है।
<तालिका सीमा = "1" सेलपैडिंग = "1" सेलस्पेसिंग = "1" शैली = "चौड़ाई: 500 पीएक्स">
<शरीर>
| इनपुट |
आउटपुट |
<टीडी>
5
5 0 0
-5 0 0
0 3 4
4 -3 0
2 2 -2
0.000 0.000 0.000 |