अनुक्रम के केवल हैश की गणना करने के बजाय, हम इसके प्रत्येक उपसर्ग पर मान संग्रहीत कर सकते हैं। ध्यान दें कि ये संबंधित उपसर्ग के बराबर अनुक्रमों के लिए हैश मान होंगे।
इस तरह की संरचना के साथ, आप इस अनुक्रम के किसी भी उपखंड के लिए हैश मान की शीघ्रता से गणना कर सकते हैं (उपसर्ग योग के समान)।
यदि हम उपखंड [l;r] के हैश की गणना करना चाहते हैं, तो हमें उपसर्ग r पर हैश लेने की आवश्यकता है और उपसर्ग l-1 पर हैश को r-l+1 की शक्ति से p से गुणा करके घटाना होगा। ऐसा क्यों है यह स्पष्ट हो जाता है यदि आप उपसर्गों पर मान लिखते हैं और देखते हैं कि क्या होता है। मुझे उम्मीद है कि आप इस तस्वीर को देखकर सफल होंगे।
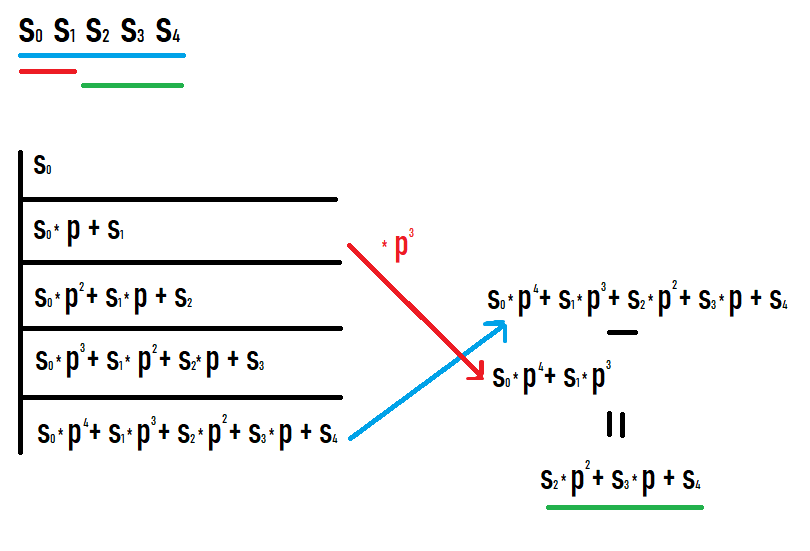
इस तरह की कार्रवाइयों के परिणामस्वरूप, हमें मूल अनुक्रम के उपखंड का हैश मिलता है। इसके अलावा, यह हैश उसके बराबर है अगर इसे इस उपखंड के बराबर अनुक्रम से हैश के रूप में माना जाता है (अन्य मूल्यों के साथ तुलना करने के लिए डिग्री या इस तरह के कोई अतिरिक्त रूपांतरण की आवश्यकता नहीं है)।
यहां दो बिंदु स्पष्ट किए जाने हैं:
1) जल्दी से p से घात r-l+1 से गुणा करने के लिए, p modulo mod की सभी संभावित शक्तियों की पूर्व गणना करना आवश्यक है।
2) यह याद रखना चाहिए कि हम सभी गणना मॉडुलो मोडुलो करते हैं, और इसलिए यह पता चल सकता है कि उपसर्ग हैश को घटाने के बाद, हमें एक ऋणात्मक संख्या मिलेगी। इससे बचने के लिए, आप घटाने से पहले हमेशा मॉड जोड़ सकते हैं। इसके अलावा, गुणा और सभी जोड़ के बाद सापेक्ष मान लेना न भूलें।
कोड में यह ऐसा दिखाई देता है:
#शामिल <बिट्स/stdc++.h>
नेमस्पेस एसटीडी का उपयोग करना;
टाइपपीफ लॉन्ग लॉन्ग;
कास्ट इंट मैक्सएन = 1000003;
// आधार और हैश मॉड्यूल
डालूँगा पी, मॉड;
// उपसर्ग हैश और प्रतिपादक p
एच [मैक्सएन], पॉज़ [मैक्सएन];
// उपखंड [एल; आर] के हैश की गणना
ll get_segment_hash(int l, int r) {
वापसी (एच [आर] + मॉड - एच [एल - 1] * पॉज़ [आर - एल + 1]% मॉड)% मॉड;
}
मुख्य प्रवेश बिंदु()
{
// किसी तरह पी और मॉड प्राप्त करें
// पूर्व-गणना शक्तियां पी
पाउ [0] = 1;
के लिए (int i = 0; i < MAXN; i++)
पॉज़ [i] = (पॉज़ [i - 1] * p)% मॉड;
//
// मुख्य समस्या समाधान
//
वापसी 0;
}