क्रमबद्ध करें
इंसर्शन सॉर्ट (इंसर्शन सॉर्ट) — ;सॉर्टिंग एल्गोरिदम जिसमें इनपुट अनुक्रम के तत्वों को एक बार में देखा जाता है, और प्रत्येक नए आने वाले तत्व को पहले से सॉर्ट किए गए तत्वों के बीच उपयुक्त स्थान पर रखा जाता है।
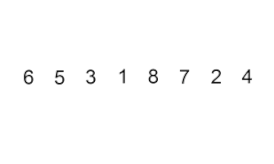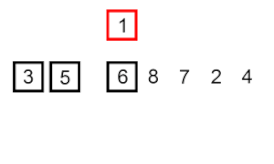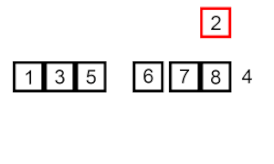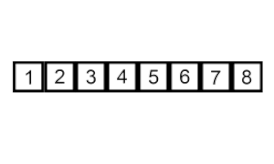
सॉर्ट डालें – यह एक बहुत ही सरल लेकिन अकुशल एल्गोरिथम है जिसके कई विशिष्ट फायदे हैं जो इसे कई अन्य आम तौर पर अधिक कुशल एल्गोरिदम विकसित होने के बाद भी प्रासंगिक बनाते हैं।
इंसर्शन सॉर्ट के साथ, आपको सॉर्ट करने से पहले संपूर्ण ऐरे को सामने रखने की आवश्यकता नहीं है। एल्गोरिथ्म छँटाई के दौरान एक समय में एक तत्व प्राप्त कर सकता है। यह बहुत आसान है यदि हमें छँटाई के दौरान और तत्वों को जोड़ने की आवश्यकता है। एल्गोरिदम नए तत्व को "फिर से निष्पादित" किए बिना सही स्थान पर सम्मिलित करेगा संपूर्ण सरणी को क्रमित करना।
छोटे (~10 तत्वों) डेटासेट पर इसकी दक्षता के कारण सम्मिलन सॉर्ट का उपयोग व्यवहार में किया जा सकता है।
समस्या यह है: सरणी का एक हिस्सा है जो पहले से ही सॉर्ट किया गया है, और आप ऑर्डर बनाए रखते हुए सरणी के शेष तत्वों को सॉर्ट किए गए भाग में सम्मिलित करना चाहते हैं। ऐसा करने के लिए, एल्गोरिथ्म के प्रत्येक चरण में, हम इनपुट डेटा तत्वों में से एक का चयन करते हैं और इसे सरणी के पहले से ही सॉर्ट किए गए भाग में वांछित स्थिति में डालते हैं, जब तक कि पूरे इनपुट डेटा सेट को सॉर्ट नहीं किया जाता है। इनपुट सरणी से अगले तत्व का चयन करने की विधि मनमाना है, लेकिन आमतौर पर (और एक स्थिर छँटाई एल्गोरिथ्म प्राप्त करने के लिए), इनपुट सरणी में उनकी उपस्थिति के क्रम में तत्वों को डाला जाता है।
इस एल्गोरिथम का एल्गोरिथम कार्यान्वयन
<पूर्व>
// अशक्त तत्व को पहले से ही क्रमबद्ध अनुक्रम माना जाता है।
// इसलिए, लूप 1 से शुरू होता है
I के लिए लूप=1 से N-1 चरण 1
एक्स = ए [मैं]
जे = मैं
WHEN J>0 AND A[J-1]>X // डालने के लिए जगह की तलाश में
एक्सचेंज ए[जे],ए[जे-1]
जे = जे -1
अलविदा
ए [जे] = एक्स
अगला मैं
कम्प्यूटेशनल जटिलता:
\(\displaystyle O(n^{2})\)।