सबरूटीन्स। प्रत्यावर्तन



यह समझा जाना चाहिए कि फ़ंक्शन कॉल में कुछ अतिरिक्त ओवरहेड शामिल होते हैं, इसलिए एक गैर-पुनरावर्ती फैक्टोरियल गणना थोड़ी तेज़ होगी। 
निष्कर्ष: जहां आप एक सरल पुनरावृत्ति एल्गोरिथ्म के साथ एक कार्यक्रम लिख सकते हैं, बिना पुनरावर्तन के, तो आपको बिना पुनरावर्तन के लिखने की आवश्यकता है। लेकिन फिर भी, समस्याओं का एक बड़ा वर्ग है जहाँ कम्प्यूटेशनल प्रक्रिया केवल पुनरावर्तन द्वारा कार्यान्वित की जाती है।
दूसरी ओर, पुनरावर्ती एल्गोरिदम अक्सर अधिक समझने योग्य होते हैं।
 

Training problem

पुनरावर्तन और पुनरावृत्ति

एक प्रक्रिया या कार्य में इसके भीतर दूसरी प्रक्रिया के लिए कॉल हो सकती है। समेत, सबरूटीन खुद को कॉल कर सकता है। इस मामले में, कंप्यूटर परवाह नहीं करता। साथ ही, हमेशा की तरह, वह उन आदेशों को लगातार निष्पादित करता है जो उसे ऊपर से नीचे तक मिलते हैं।

अगर आपको गणित याद है, तो आप गणितीय आगमन के सिद्धांत से मिल सकते हैं। यह इस प्रकार है:

प्रत्येक प्राकृतिक n if
के लिए एक निश्चित कथन सत्य है     1. यह n = 1 और
के लिए मान्य है     2. किसी भी स्वाभाविक प्राकृतिक n = k के लिए कथन की वैधता से यह अनुसरण करता है कि यह n = k+1.
के लिए सत्य है
प्रोग्रामिंग में, इस तकनीक को रिकर्सन
कहा जाता है
रिकर्सन दिए गए सरल आधार मामलों के आधार पर सेट के संदर्भ में वस्तुओं के एक सेट को परिभाषित करने का एक तरीका है।

रिकर्सिव को प्रक्रिया (फ़ंक्शन) भी कहा जाएगा जो स्वयं को सीधे या अन्य प्रक्रियाओं और कार्यों के माध्यम से कॉल करता है
एक पुनरावर्ती प्रक्रिया का एक उदाहरण: <पूर्व> <कोड> प्रक्रिया आरईसी (ए: पूर्णांक); शुरू     अगर एक > 0 तब         आरईसी (ए - 1);     लिखना एक); अंत; योजनाबद्ध रूप से, पुनरावर्तन के कार्य को फ़्लोचार्ट द्वारा दर्शाया जा सकता है

 
Rec() प्रक्रिया को पैरामीटर 3 के साथ निष्पादित किया जाता है। फिर, पैरामीटर 3 के साथ प्रक्रिया के अंदर, पैरामीटर 2 के साथ प्रक्रिया को कॉल किया जाता है, और इसी तरह, जब तक पैरामीटर 0 के साथ प्रक्रिया को कॉल नहीं किया जाता है। जब प्रक्रिया के साथ पैरामीटर 0 कहा जाता है, पुनरावर्ती कॉल पहले से नहीं होगा और पैरामीटर 0 वाली प्रक्रिया संख्या 0 को प्रिंट करेगी और समाप्त हो जाएगी। फिर नियंत्रण को पैरामीटर 1 के साथ प्रक्रिया में वापस स्थानांतरित कर दिया जाता है, यह नंबर 1 को प्रिंट करके अपना काम भी पूरा करता है, और इसी तरह। पैरामीटर 3 के साथ प्रक्रिया से पहले। 

जब तक वे अपना काम पूरा नहीं कर लेते, तब तक सभी प्रक्रियाओं को स्मृति में संग्रहीत किया जाता है। समवर्ती प्रक्रियाओं की संख्या को पुनरावर्तन गहराई कहा जाता है।

Training problem

पुनरावर्तन। यह क्या है?

हमने देखा है कि पुनरावर्तन एक उपनेमका में निहित निर्देशों का बार-बार निष्पादन है। और यह बदले में चक्र के कार्य के समान है। ऐसी प्रोग्रामिंग भाषाएं हैं जिनमें लूप निर्माण बिल्कुल अनुपस्थित है, उदाहरण के लिए, प्रोलॉग। 
आइए for लूप के संचालन का अनुकरण करने का प्रयास करें। 
लूप के लिए एक स्टेप काउंटर वेरिएबल होता है। एक पुनरावर्ती उपनेमका में, ऐसे चर को एक पैरामीटर के रूप में पारित किया जा सकता है। <पूर्व> // लूपइमिटेशन () प्रक्रिया दो मापदंडों के साथ // पहला पैरामीटर – स्टेप काउंटर, दूसरा पैरामीटर - चरणों की कुल संख्या प्रक्रिया लूपइमिटेशन (i, n: पूर्णांक); शुरू     राइटलन ('हैलो एन', आई); // ऑपरेटर i के किसी भी मूल्य के लिए दोहराया जाना है     अगर मैं < n तब // जब तक लूप काउंटर मान n के बराबर न हो जाए,         लूपइमिटेशन (i + 1, n); // प्रक्रिया का एक नया उदाहरण कॉल करें, पैरामीटर i+1 के साथ (अगले मान i में संक्रमण) अंत;

Training problem

पुनरावर्तन। साइकिल सिमुलेशन

रिकर्सन को समझने के लिए, आपको रिकर्सन को समझने की जरूरत है...
 
<कोड>पुनरावृत्ति प्रोग्रामिंग में — व्यापक अर्थों में — डेटा प्रोसेसिंग का संगठन, जिसमें कार्रवाइयाँ कई बार दोहराई जाती हैं, बिना खुद को कॉल किए (विपरीत  %BA%D1%83%D1%80%D1%81%D0%B8%D1%8F" title="Recursion" >पुनरावृत्ति)। संकीर्ण अर्थ में — एक चरण चक्रीय डेटा संसाधन प्रक्रिया। 
वर्तमान चरण (पुनरावृत्ति) पर अक्सर पुनरावृत्त एल्गोरिदम पिछले चरणों में गणना किए गए समान ऑपरेशन या क्रिया के परिणाम का उपयोग करते हैं।  ऐसी गणनाओं का एक उदाहरण पुनरावृत्ति संबंधों की गणना है। 
पुनरावर्ती मान का एक सरल उदाहरण भाज्य है: \(N!=1 \cdot 2 \cdot 3 \cdot \ ... \ \cdot N\) प्रत्येक चरण (पुनरावृत्ति) पर मूल्य की गणना \(N=N \cdot i\) है।  \(N\) के मान की गणना करते समय, हम पहले से संग्रहीत मान लेते हैं \(N\)।< बीआर />
किसी संख्या के क्रमगुणन को पुनरावर्ती सूत्र:
का उपयोग करके भी वर्णित किया जा सकता है


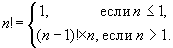
आप देख सकते हैं कि यह विवरण एक पुनरावर्ती क्रिया से अधिक कुछ नहीं है।
यहाँ पहली पंक्ति (\(n <= 1\)) — यह आधार मामला है (पुनरावृत्ति की अंतिम स्थिति) और दूसरी पंक्ति अगले चरण के लिए संक्रमण है। 
  <तालिका सीमा = "1" सेलपैडिंग = "1" सेलस्पेसिंग = "1" शैली = "चौड़ाई: 500 पीएक्स"> <शरीर>
रिकर्सिव फैक्टोरियल फंक्शन इस तरह दिखेगा सामान्य, गैर-पुनरावर्ती तरीके से फैक्टोरियल खोजने के लिए एल्गोरिदम की तुलना करें
फ़ंक्शन फैक्टोरियल (एन: पूर्णांक): पूर्णांक;
शुरू
    अगर एन > 1 फिर
        क्रमगुणित := n * क्रमगुणित(n - 1)
    वरना
        क्रमगुणित := 1;
अंत;		 x := 1;
for i := 2 to n do
    x := x * i;
लेख (एक्स);