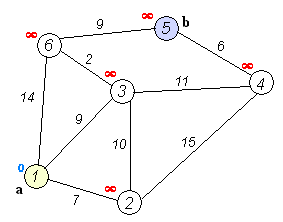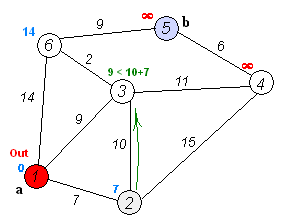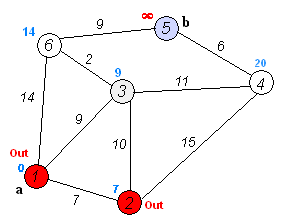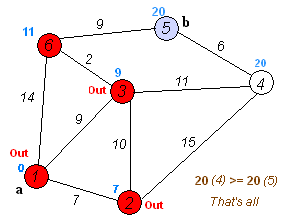
Dato un grafo pesato orientato o non orientato con n vertici e m archi. I pesi di tutti i bordi sono non negativi. Alcuni vertici iniziali s sono specificati. Devi trovare le lunghezze dei percorsi più brevi dal vertice s a tutti gli altri vertici e fornire anche un modo per stampare i percorsi più brevi stessi.
Questo problema è chiamato "problema del percorso più breve a origine singola" (problema dei cammini minimi a sorgente singola).
Esegue le stesse attività di 1-K BFS, ma senza tener conto di K. Inoltre, come 1-K BFS, non gestisce correttamente i fronti negativi
Algoritmo:
L'algoritmo di Dijkstra stesso consiste di N iterazioni. Alla successiva iterazione, il vertice V con la minima distanza da esso tra i vertici non ancora marcati, questo vertice diventa marcato e da esso si verificano rilassamenti dei vertici vicini.
il comportamento asintotico finale dell'algoritmo è: O(n
2+ m)