Per capire la ricorsione, devi capire la ricorsione...
Iterazione nella programmazione — in senso lato — organizzazione del trattamento dei dati, in cui le azioni si ripetono molte volte, senza portare a chiamate a se stesse (a differenza di %BA%D1%83%D1%80%D1%81%D0%B8%D1%8F" title="Ricorsione" >Ricorsioni). In senso stretto — processo di elaborazione dei dati ciclico in un'unica fase.
Spesso gli algoritmi iterativi nella fase corrente (iterazione) utilizzano il risultato della stessa operazione o azione calcolata nelle fasi precedenti. Un esempio di tali calcoli è il calcolo delle relazioni di ricorrenza.
Un semplice esempio di valore ricorsivo è il fattoriale:
\(N!=1 \cdot 2 \cdot 3 \cdot \ ... \ \cdot N\)
Il calcolo del valore ad ogni passo (iterazione) è
\(N=N \cdot i\) . Quando calcoliamo il valore di
\(N\), prendiamo il valore già memorizzato
\(N\).
Il fattoriale di un numero può anche essere descritto usando la
formula ricorrente:
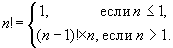
Potresti notare che questa descrizione non è altro che una funzione ricorsiva.
Qui la prima riga (
\(n <= 1\)) — questo è il caso base (condizione finale della ricorsione) e la seconda riga è la transizione al passaggio successivo.
| La funzione fattoriale ricorsiva sarebbe simile a questa |
Confronta l'algoritmo per trovare il fattoriale nel solito modo non ricorsivo |
|
int Fattoriale(int n){
se (n > 1)
return n * Fattoriale(n - 1);
altrimenti restituisce 1;
}
|
x = 1;
per (i = 2; i <= n; i++)
x = x * io;
printf("%d",x);
|
Dovrebbe essere chiaro che le chiamate di funzione comportano un sovraccarico aggiuntivo, quindi un calcolo fattoriale non ricorsivo sarà leggermente più veloce.
Conclusione: dove puoi scrivere un programma con un semplice algoritmo iterativo, senza ricorsione, allora devi scrivere senza ricorsione. Tuttavia, esiste un'ampia classe di problemi in cui il processo computazionale è implementato solo mediante ricorsione.
D'altra parte, gli algoritmi ricorsivi sono spesso più comprensibili.