Problem
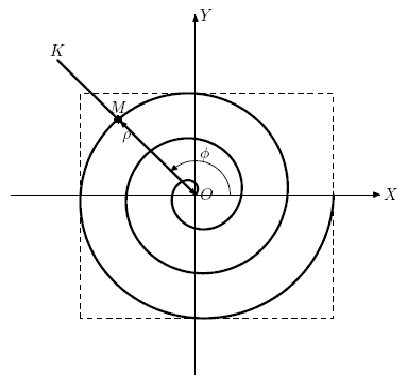
Dima è recentemente entrato a far parte dell'Istituto di ricerca sulle curve piatte. Come suggerisce il nome di questo istituto di ricerca, è impegnato in varie ricerche nel campo delle curve piane. Di recente, il capo di Dimin, Georgy, ha incontrato una curva molto interessante, che, come si è scoperto dopo alcune ricerche, è nota come spirale di Archimede. La spirale di Archimede è una curva piana raffigurante la traiettoria del punto M, che si muove uniformemente lungo il raggio OK con origine in O, mentre il raggio OK stesso ruota uniformemente attorno al punto O (vedi figura). In altre parole, la distanza dall'origine ρ = OM linearmente dipendente dall'angolo di rotazione .phi. raggio OK. In questo caso, la rotazione della semiretta OK dello stesso angolo corrisponde allo stesso incremento di distanza ρ.
Il movimento del punto M può essere impostato utilizzando una serie di parametri:
• angolo di rotazione iniziale .alpha. fascio OK (misurato in gradi in senso antiorario rispetto alla direzione positiva dell'asse OX);
• velocità angolare .omega. raggio OK (misurato in gradi per unità di tempo);
• la distanza iniziale R dal punto M all'origine (punto O);
• velocità V del punto M lungo il raggio OK.
Se, impostando questi parametri, non limitiamo il tempo di spostamento del punto M, allora otteniamo una curva infinita, piuttosto difficile da esplorare. Pertanto, Dima ha deciso di limitarsi a studiare una parte di questa curva, quella che si ottiene quando il punto M si sposta dall'istante zero all'istante T. Il problema che Dima risolve è trovare un rettangolo del area minima con lati paralleli agli assi coordinati, in cui è inscrivibile.
Devi scrivere un programma che trovi il rettangolo desiderato
Input
Il file di input contiene quattro numeri interi: ω (1 ≤ omega; ≤ 100), V (1 ≤ V ≤ 100), R (0 ≤ R ≤ 100) e T (1 ≤ T ≤ 1000). In questo problema si presume che l'angolo di rotazione iniziale .alpha. è zero.
Uscita
Nella prima riga del file di output stampa due numeri reali — le coordinate dell'angolo in basso a sinistra del rettangolo desiderato e nella seconda riga — coordinate dell'angolo in alto a destra del rettangolo desiderato.
La risposta sarà considerata corretta se il valore di ciascuna delle coordinate differisce dal valore reale di non più di 10-5.
| Input |
Uscita |
| 60 10 0 18 |
-150.3028434716 -165.2754877824
180.0000000000 135.3362037333
|
Team Olympiad, VKOSHP, 2008, Problema I