Ordinamenti quadratici


Ordinamenti quadratici

Ordinamento - sta riorganizzando gli elementi di un array (lista) in un determinato ordine.

Bubble method (bubble sort) o ordinamento per semplici scambi).
Un classico immortale del genere. Il principio di funzionamento è semplice: aggiriamo l'array dall'inizio alla fine, scambiando contemporaneamente elementi vicini non ordinati. Come risultato del primo passaggio all'ultimo posto, "si apre" elemento massimo. Ora aggiriamo nuovamente la parte non ordinata dell'array (dal primo elemento al penultimo) e cambiamo i vicini non ordinati lungo il percorso. Il secondo elemento più grande sarà al penultimo posto. Continuando con lo stesso spirito, aggireremo la parte non ordinata in continua diminuzione dell'array, spingendo i massimi trovati fino alla fine.
 
Fonte

Implementazione algoritmica di questo algoritmo
CICLO PER J=1 TO N-1 PASSO 1
   F=0
   LOOP FOR I=1 TO N-J-1 PASSO 1
     SE A[I] > A[I+1] ALLORA
       SCAMBIA A[I],A[I+1]
       F=1
   PROSSIMO I
   IF F=0 THEN EXIT THE LOOP // se non ci sono stati scambi durante il passaggio,
  // che significa tutti gli elementi
  // disposti in ordine
 PROSSIMO J
Complessità di questo algoritmo: \(\displaystyle O(n^{2})\).


Ulteriori informazioni utili: Articolo di Wikipedia.

 

Training problem

sorta di bolla

Inserisci ordinamento

Ordinamento per inserzione (Ordinamento per inserzione) —  ;algoritmo di ordinamento in cui gli elementi della sequenza di input vengono cercati uno alla volta e ogni nuovo elemento in arrivo viene posizionato nella posizione appropriata tra gli elementi precedentemente ordinati.


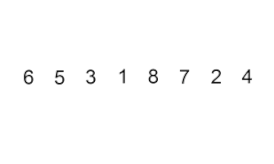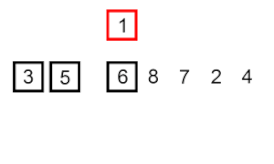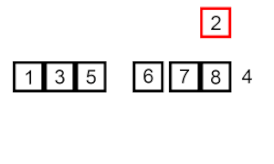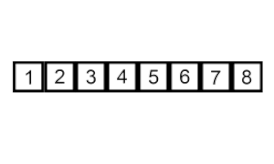
Inserisci ordinamento – è un algoritmo molto semplice ma inefficiente che tuttavia presenta diversi vantaggi specifici che lo rendono rilevante anche dopo che sono stati sviluppati molti altri algoritmi generalmente più efficienti.

Con l'ordinamento per inserzione, non è necessario disporre dell'intero array in primo piano prima dell'ordinamento. L'algoritmo può ricevere un elemento alla volta durante l'ordinamento. Questo è molto utile se dobbiamo aggiungere altri elementi durante l'ordinamento. L'algoritmo inserirà il nuovo elemento nel posto giusto senza "rieseguire" ordinando l'intero array.

Insertion sort può essere utilizzato nella pratica grazie alla sua efficienza su set di dati piccoli (~10 elementi).

Il problema è questo: c'è una parte dell'array che è già ordinata, e tu vuoi inserire i restanti elementi dell'array nella parte ordinata, mantenendo l'ordine. Per fare ciò, ad ogni passo dell'algoritmo, selezioniamo uno degli elementi di dati di input e lo inseriamo nella posizione desiderata nella parte già ordinata dell'array, finché l'intero set di dati di input non viene ordinato. Il metodo di selezione dell'elemento successivo dall'array di input è arbitrario, ma di solito (e per ottenere un algoritmo di ordinamento stabile), gli elementi vengono inseriti nell'ordine in cui appaiono nell'array di input.

Implementazione algoritmica di questo algoritmo
// L'elemento nullo è considerato una sequenza già ordinata.
// Pertanto, il ciclo inizia da 1
CICLO PER I=1 TO N-1 PASSO 1
   X=LA[I]
   J=I
   WHEN J>0 AND A[J-1]>X //cerco un punto da inserire
     SCAMBIO A[J],A[J-1]
     J=J-1
   FINE CIAO
   A[J]=X
 PROSSIMO I
Complessità computazionale: \(\displaystyle O(n^{2})\).

Training problem

Ordinamento per inserzione