再帰を理解するには、再帰を理解する必要があります...
プログラミングにおける
反復—広い意味では、データ処理の組織。(%BA%D1%83%D1%80%D1%81%D0%B8%D1%8F" title="再帰" とは異なり、自身への呼び出しを引き起こすことなく、アクションが何度も繰り返されます) > 再帰)。狭義では、ワンステップの循環データ処理プロセス。
多くの場合、現在のステップ (反復) での反復アルゴリズムは、前のステップで計算された同じ操作またはアクションの結果を使用します。 そのような計算の一例は漸化関係の計算です。
再帰的な値の簡単な例は階乗です:
\(N!=1 \cdot 2 \cdot 3 \cdot \ ... \ \cdot N\)
各ステップ (反復) での値の計算は
\(N=N \cdot i\) です。
\(N\) の値を計算するときは、すでに保存されている値
\(N\) が使用されます。 >.
数値の階乗は、
漸化式を使用して記述することもできます。
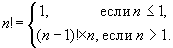
この説明は単なる再帰関数に過ぎないことに気づくかもしれません
。
ここで、最初の行 (
\(n <= 1\)) —これは基本ケース (再帰の終了条件) で、2 行目は次のステップへの移行です。
<本体>
| 再帰階乗関数は次のようになります |
通常の非再帰的な方法で階乗を求めるアルゴリズムを比較します |
関数 Factorial(n: 整数): 整数;
始める
n > の場合1 その後
階乗 := n * 階乗(n - 1)
その他
階乗 := 1;
終了; |
x := 1;
for i := 2 to n do
x := x * i;
writeln(x); |
関数呼び出しには追加のオーバーヘッドがかかるため、非再帰階乗計算の方が若干高速になることを理解してください。
結論:再帰なしで単純な反復アルゴリズムを使用してプログラムを作成できる場合は、再帰なしで作成する必要があります。しかしそれでも、計算プロセスが再帰によってのみ実装される問題の大きなクラスが存在します。
一方、再帰的アルゴリズムの方が理解しやすい場合が多い
です。
Problem
指定された自然数の桁数を返す関数 K(n) を定義します n:
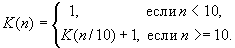
自然数nの桁数を計算する再帰関数を書きなさい。
Запрещенные операторы: for;while;until