n 個の要素の k による組み合わせは、n 個の要素から形成できる複合物であり、各接続で k 個の要素が集まります。一方、接続は要素自体によってのみ互いに異なります (配置順序の違いは考慮されません)。
たとえば、次の組み合わせは、3 つの要素 (a,b,c)(a,b,c) 2 つから形成できます: ab,ac,bc。
n 要素から k によって形成できるすべての可能な組み合わせの数は、記号

次の式で計算されます:
組み合わせの数を確認するには 2 つの方法があります

1. n!、k!、(n – k)! を見つけてください。上記の式に従って、数量を計算しますが、オーバーフローの可能性があるため、このメソッドは n <= 12 で使用できます。
2.動的プログラミングを使用します。
DP はパスカルの三角形のように見え、上部と端に 1 があり、各数値はその上の 2 つの数値の合計に等しくなります。
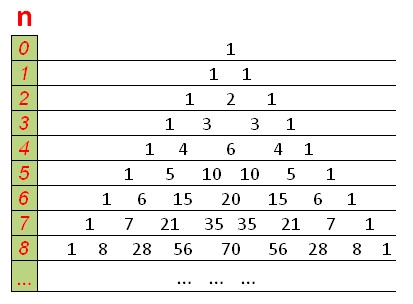
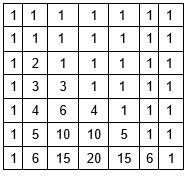
O(n ^2 ) の動的計画法を使用して組み合わせの数をカウントする関数:
int C(int n, int k)
{
ベクトル<ベクトル<int> > dp(n + 1, ベクトルint>(n + 1, 1)); // サイズ (n + 1, n + 1) の dp 配列を作成します
for (int i = 0; i <= n; i++) // 配列の i 行目を埋めます
{
for (int j = 1; j < i; j++)
{
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; //(i - 1; j - 1) と (i - 1; j) を通じて (i;j) の位置を再計算します
}
}
return dp[n][k]; //戻り値
}