並べ替えを挿入
挿入並べ替え (挿入並べ替え) — ; 入力シーケンスの要素が一度に 1 つずつ検索され、新しく入力された各要素が、以前に並べ替えられた要素の適切な場所に配置される並べ替えアルゴリズム。
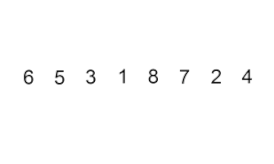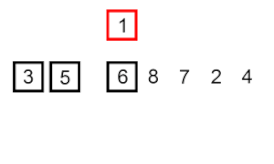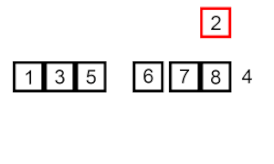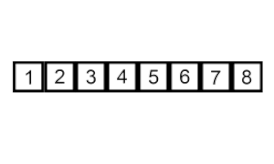
並べ替えを挿入 –これは非常に単純ですが非効率なアルゴリズムですが、他の多くの一般的に効率的なアルゴリズムが開発された後でも、このアルゴリズムを意味のあるものにするいくつかの特定の利点があります。
挿入ソートを使用すると、ソートの前に配列全体を事前に用意する必要はありません。アルゴリズムは、並べ替え中に一度に 1 つの要素を受け取ることができます。これは、 並べ替え中に要素を追加する必要がある場合に非常に便利です。 アルゴリズムは、「再実行」せずに新しい要素を正しい場所に挿入します。配列全体を並べ替えます。
挿入ソートは、小さい (要素数 10 個程度) データセットで効率が良いため、実際に使用できます。
問題は、配列の一部がすでにソートされており、順序を維持しながら配列の残りの要素をソートされた部分に挿入したいということです。これを行うには、アルゴリズムの各ステップで入力データ要素の 1 つを選択し、入力データ セット全体が並べ替えられるまで、配列の既に並べ替えられた部分の目的の位置にそれを挿入します。入力配列から次の要素を選択する方法は任意ですが、通常 (安定した並べ替えアルゴリズムを得るために)、要素は入力配列に出現する順序で挿入されます。
このアルゴリズムのアルゴリズム実装
<プレ>
// null 要素は、すでにソートされたシーケンスとみなされます。
// したがって、ループは 1 から始まります
I=1 ~ N-1 のループ ステップ 1
X=A[I]
J=I
WHEN J>0 AND A[J-1]>X //挿入する場所を探しています
交換A[J]、A[J-1]
J=J-1
エンドバイ
A[J]=X
次へ
計算複雑さ:
\(\displaystyle O(n^{2})\)。