지정된 에지 가중치가 있는 그래프의 최소 스패닝 트리 예:
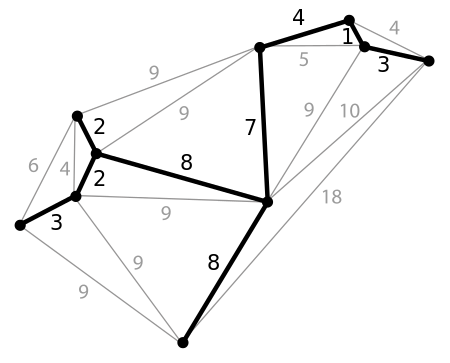
Kruskal의 알고리즘:
1) 가중치로 가장자리 정렬 감소하지 않는 순서로.
2) 우리는 n개의 트리 목록을 형성합니다(각 정점은 트리입니다).
3) 이러한 트리를 최소 스패닝 트리로 결합하는 프로세스를 시작합니다.
모든 에지가 트래버스되고 현재 에지의 끝이 다른 하위 트리에 속하는 경우 이러한 하위 트리가 병합됩니다.
4) 모든 가장자리의 열거가 끝나면 모든 정점이 동일한 하위 트리에 속합니다.