조합


n개의 원소와 k의 조합은 n개의 원소로부터 형성될 수 있는 화합물이며, 각 연결에서 k개의 원소를 수집합니다. 연결은 요소 자체에 의해서만 서로 다릅니다(배열 순서의 차이는 고려되지 않음).
 
예를 들어, 다음 조합은 3개의 요소 (a,b,c)(a,b,c)에서 각각 2개씩 형성될 수 있습니다: ab,ac,bc.
 
n개의 요소로부터 k에 의해 형성될 수 있는 모든 가능한 조합의 수는  다음 공식으로 계산됩니다.
<사업부> 
조합의 수를 찾는 방법에는 두 가지가 있습니다. 
 
<사업부>1. n!, k!, (n – k)를 찾아라! 위 공식에 따라 수량을 계산하지만 – 오버플로 가능성으로 인해 이 방법은 n <= 12와 함께 사용할 수 있습니다.
 
<사업부>2. 동적 프로그래밍으로.
 
DP는 위쪽과 가장자리에 삼각형이 있는 파스칼의 삼각형 모양이며 각 숫자는 그 위에 있는 두 숫자의 합과 같습니다.





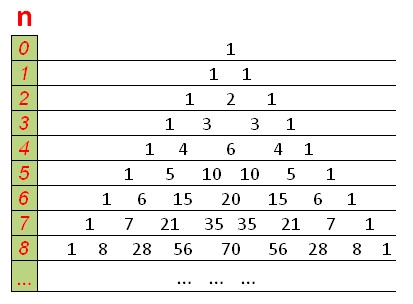
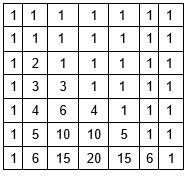
O(n ^2 )에서 동적 프로그래밍을 사용하여 조합의 수를 세는 함수:

정수 C(정수 n, 정수 스팬 > k)
{
vector<vector<int> > dp(n + 1, 벡터<int>(n + 1, 1)); // (n + 1, n + 1) 크기의 dp 배열 생성
for (int i = 0; i <= n; i++) // 배열의 i번째 줄을 채웁니다.
{
for (int j = 1; j < i; j++)
{
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; //(i - 1; j - 1) 및 (i - 1; j)를 통해 (i;j) 위치 재계산 
}
}
반품 dp[n][k]; //반환 값 
}

Training problem

조합 수